Morley's Theorem

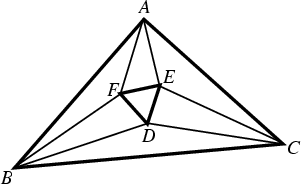
The points of intersection of the adjacent Trisectors of the Angles of any Triangle $\Delta ABC$ are the Vertices of an Equilateral Triangle $\Delta DEF$ known as Morley's Triangle. Taylor and Marr (1914) give two geometric proofs and one trigonometric proof.

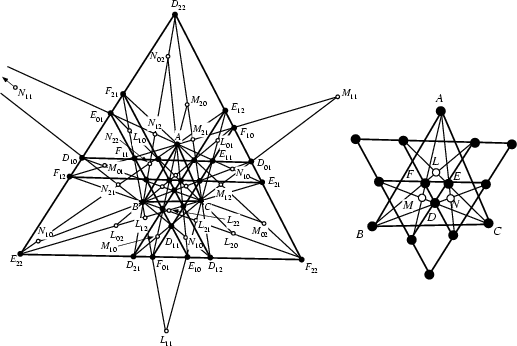
A generalization of Morley's Theorem was discovered by Morley in 1900 but first published by Taylor and Marr (1914). Each Angle of a Triangle $\Delta ABC$ has six trisectors, since each interior angle trisector has two associated lines making angles of 120° with it. The generalization of Morley's theorem states that these trisectors intersect in 27 points (denoted $D_{ij}$, $E_{ij}$, $F_{ij}$, for $i,j=0$, 1, 2) which lie six by six on nine lines. Furthermore, these lines are in three triples of Parallel lines, ($D_{22}E_{22}$, $E_{12}D_{21}$, $F_{10}F_{01}$), ($D_{22}F_{22}$, $F_{21}D_{12}$, $E_{01}E_{10}$), and ($E_{22}F_{22}$, $F_{12}E_{21}$, $D_{10}D_{01}$), making Angles of 60° with one another (Taylor and Marr 1914, Johnson 1929, p. 254).

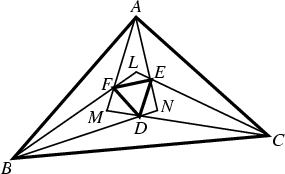
Let $L$, $M$, and $N$ be the other trisector-trisector intersections, and let the 27 points $L_{ij}$, $M_{ij}$, $N_{ij}$ for $i,j=0$, 1, 2 be the Isogonal Conjugates of $D$, $E$, and $F$. Then these points lie 6 by 6 on 9 Conics through $\Delta ABC$. In addition, these Conics meet 3 by 3 on the Circumcircle, and the three meeting points form an Equilateral Triangle whose sides are Parallel to those of $\Delta DEF$.

See also Conic Section, Morley Centers, Trisection

References

Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 47-50, 1967.

Gardner, M. Martin Gardner's New Mathematical Diversions from Scientific American. New York: Simon and Schuster, pp. 198 and 206, 1966.

Honsberger, R. ``Morley's Theorem.'' Ch. 8 in Mathematical Gems I. Washington, DC: Math. Assoc. Amer., pp. 92-98, 1973.

Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 253-256, 1929.

Kimberling, C. ``Hofstadter Points.'' Nieuw Arch. Wiskunder 12, 109-114, 1994.

Marr, W. L. ``Morley's Trisection Theorem: An Extension and Its Relation to the Circles of Apollonius.'' Proc. Edinburgh Math. Soc. 32, 136-150, 1914.

Oakley, C. O. and Baker, J. C. ``The Morley Trisector Theorem.'' Amer. Math. Monthly 85, 737-745, 1978.

Pappas, T. ``Trisecting & the Equilateral Triangle.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 174, 1989.

Taylor, F. G. ``The Relation of Morley's Theorem to the Hessian Axis and Circumcentre.'' Proc. Edinburgh Math. Soc. 32, 132-135, 1914.

Taylor, F. G. and Marr, W. L. ``The Six Trisectors of Each of the Angles of a Triangle.'' Proc. Edinburgh Math. Soc. 32, 119-131, 1914.