|
|
|
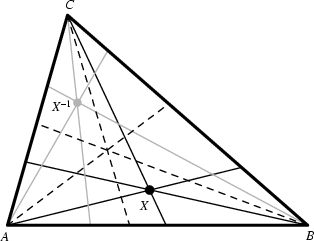
The isogonal conjugate ![]() of a point
of a point ![]() in the plane of the Triangle
in the plane of the Triangle ![]() is constructed by
reflecting the lines
is constructed by
reflecting the lines ![]() ,
, ![]() , and
, and ![]() about the Angle Bisectors at
about the Angle Bisectors at ![]() ,
, ![]() , and
, and ![]() . The
three reflected lines Concur at the isogonal conjugate. The Trilinear Coordinates of the
isogonal conjugate of the point with coordinates
. The
three reflected lines Concur at the isogonal conjugate. The Trilinear Coordinates of the
isogonal conjugate of the point with coordinates
Isogonal conjugation maps the interior of a Triangle onto itself. This mapping transforms lines onto Conic
Sections that Circumscribe the Triangle. The type of Conic Section
is determined by whether the line ![]() meets the Circumcircle
meets the Circumcircle ![]() ,
,
The isogonal conjugate of a point on the Circumcircle is a Point at Infinity (and conversely). The sides of the Pedal Triangle of a point are Perpendicular to the connectors of the corresponding Vertices with the isogonal conjugate. The isogonal conjugate of a set of points is the Locus of their isogonal conjugate points.
The product of Isotomic and isogonal conjugation is a Collineation which transforms the sides of a Triangle to themselves (Vandeghen 1965).
See also Antipedal Triangle, Collineation, Isogonal Line, Isotomic Conjugate Point, Line at Infinity, Symmedian Line
References
Casey, J. A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing
an Account of Its Most Recent Extensions with Numerous Examples, 2nd rev. enl. ed. Dublin: Hodges, Figgis, & Co., 1893.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle.
Boston, MA: Houghton Mifflin, pp. 153-158, 1929.
Vandeghen, A. ``Some Remarks on the Isogonal and Cevian Transforms. Alignments of Remarkable Points of a Triangle.''
Amer. Math. Monthly 72, 1091-1094, 1965.
|
|
|
© 1996-9 Eric W. Weisstein