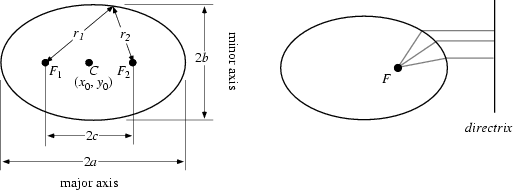
A curve which is the Locus of all points in the Plane the Sum of whose distances 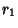 and
and 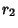 from two fixed points
from two fixed points 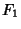 and
and 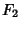 (the Foci) separated by a distance of
(the Foci) separated by a distance of 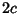 is a given Positive
constant
is a given Positive
constant 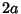 (left figure). This results in the two-center Bipolar Coordinate equation
(left figure). This results in the two-center Bipolar Coordinate equation
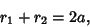 |
(1) |
where  is the Semimajor Axis and the Origin of the coordinate system is at one of the
Foci. The ellipse can also be defined as the Locus of points whose distance from the Focus
is proportional to the horizontal distance from a vertical line known as the Directrix (right figure).
is the Semimajor Axis and the Origin of the coordinate system is at one of the
Foci. The ellipse can also be defined as the Locus of points whose distance from the Focus
is proportional to the horizontal distance from a vertical line known as the Directrix (right figure).
The ellipse was first studied by Menaechmus, investigated by Euclid,  and named by Apollonius.
and named by Apollonius.  The
Focus and Directrix of an ellipse were considered by Pappus. In 1602,
Kepler
The
Focus and Directrix of an ellipse were considered by Pappus. In 1602,
Kepler  believed that the orbit of Mars
believed that the orbit of Mars  was Oval; he later discovered that it was an ellipse
with the Sun
was Oval; he later discovered that it was an ellipse
with the Sun  at one Focus. In fact, Kepler introduced the word ``Focus'' and published his
discovery in 1609. In 1705 Halley
at one Focus. In fact, Kepler introduced the word ``Focus'' and published his
discovery in 1609. In 1705 Halley  showed that the comet
showed that the comet  which is now named after him moved in an
elliptical orbit around the Sun (MacTutor Archive).
which is now named after him moved in an
elliptical orbit around the Sun (MacTutor Archive).
A ray passing through a Focus will pass through the other focus after a single bounce. Reflections not passing
through a Focus will be tangent to a confocal Hyperbola or Ellipse, depending on whether the ray
passes between the Foci or not. Let an ellipse lie along the x-Axis and find the equation of
the figure (1) where 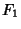 and
and 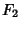 are at
are at 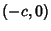 and
and 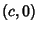 . In Cartesian Coordinates,
. In Cartesian Coordinates,
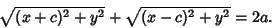 |
(2) |
Bring the second term to the right side and square both sides,
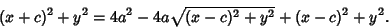 |
(3) |
Now solve for the Square Root term and simplify
Square one final time to clear the remaining Square Root,
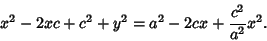 |
(5) |
Grouping the  terms then gives
terms then gives
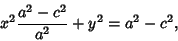 |
(6) |
which can be written in the simple form
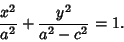 |
(7) |
Defining a new constant
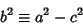 |
(8) |
puts the equation in the particularly simple form
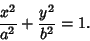 |
(9) |
The parameter  is called the Semiminor Axis by analogy with the parameter
is called the Semiminor Axis by analogy with the parameter  , which is called the
Semimajor Axis. The fact that
, which is called the
Semimajor Axis. The fact that  as defined above is actually the Semiminor Axis is easily shown by letting
as defined above is actually the Semiminor Axis is easily shown by letting
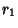 and
and 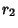 be equal. Then two Right Triangles are produced, each with Hypotenuse
be equal. Then two Right Triangles are produced, each with Hypotenuse
 , base
, base  , and height
, and height
 . Since the largest distance along the Minor Axis will be
achieved at this point,
. Since the largest distance along the Minor Axis will be
achieved at this point,  is indeed the Semiminor Axis.
is indeed the Semiminor Axis.
If, instead of being centered at (0, 0), the Center of the ellipse is at (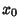 ,
,  ), equation (9) becomes
), equation (9) becomes
 |
(10) |
As can be seen from the Cartesian Equation for the ellipse, the curve can also be given by a
simple parametric form analogous to that of a Circle, but with the  and
and 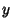 coordinates having different scalings,
coordinates having different scalings,
The unit Tangent Vector of the ellipse so parameterized is
A sequence of Normal and Tangent Vectors are plotted below for
the ellipse.
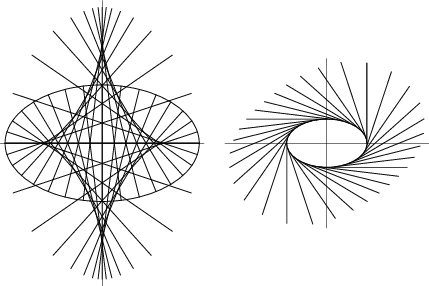
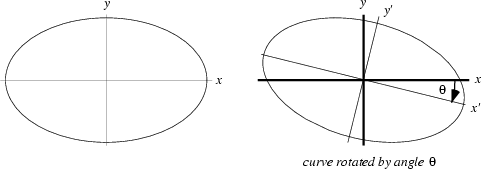
For an ellipse centered at the Origin but inclined at an arbitrary Angle 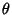 to the x-Axis, the
parametric equations are
to the x-Axis, the
parametric equations are
In Polar Coordinates, the Angle 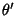 measured from the center of the ellipse is
called the Eccentric Angle. Writing
measured from the center of the ellipse is
called the Eccentric Angle. Writing 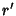 for the distance of a point from the ellipse center, the equation in
Polar Coordinates is just given by the usual
for the distance of a point from the ellipse center, the equation in
Polar Coordinates is just given by the usual
Here, the coordinates 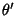 and
and 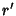 are written with primes to distinguish them from the more common polar coordinates
for an ellipse which are centered on a focus. Plugging the polar equations into the Cartesian equation (9) and
solving for
are written with primes to distinguish them from the more common polar coordinates
for an ellipse which are centered on a focus. Plugging the polar equations into the Cartesian equation (9) and
solving for 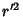 gives
gives
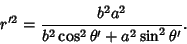 |
(18) |
Define a new constant 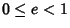 called the Eccentricity (where
called the Eccentricity (where 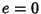 is the case of a Circle) to replace
is the case of a Circle) to replace 
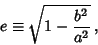 |
(19) |
from which it also follows from (8) that
Therefore (18) can be written as
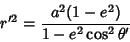 |
(23) |
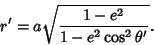 |
(24) |
If  , then
, then
![\begin{displaymath}
r' = a\{1-{\textstyle{1\over 2}}e^2\sin^2\theta'-{\textstyle{1\over 16}}e^4[5+3\cos(2\theta')]\sin^2\theta'+\ldots\},
\end{displaymath}](e_497.gif) |
(25) |
so
 |
(26) |
If 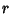 and
and 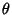 are measured from a Focus instead of from the center, as they commonly are in
orbital mechanics,
are measured from a Focus instead of from the center, as they commonly are in
orbital mechanics,  then the equations of the ellipse are
then the equations of the ellipse are
and (9) becomes
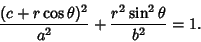 |
(29) |
Clearing the Denominators gives
 |
(30) |
 |
(31) |
Plugging in (21) and (22) to re-express  and
and  in terms of
in terms of  and
and  ,
,

|
|
![$ +a^2r^2-a^2r^2\cos^2\theta = a^2[a^2(1-e^2)].\quad$](e_506.gif)
|
(32) |
Simplifying,
![\begin{displaymath}
-r^2+[er\cos\theta-a(1-e^2)]^2 = 0
\end{displaymath}](e_507.gif) |
(33) |
![\begin{displaymath}
r = \pm [er\cos\theta-a(1-e^2)].
\end{displaymath}](e_508.gif) |
(34) |
The sign can be determined by requiring that 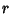 must be Positive. When
must be Positive. When 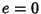 , (34) becomes
, (34) becomes 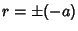 , but
since
, but
since  is always Positive, we must take the Negative sign, so (34) becomes
is always Positive, we must take the Negative sign, so (34) becomes
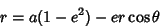 |
(35) |
 |
(36) |
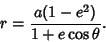 |
(37) |
The distance from a Focus to a point with horizontal coordinate  is found from
is found from
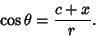 |
(38) |
Plugging this into (37) yields
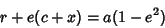 |
(39) |
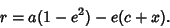 |
(40) |
Summarizing relationships among the parameters characterizing an ellipse,
The Eccentricity can therefore be interpreted as the position of the Focus as a fraction of the
Semimajor Axis.
In Pedal Coordinates with the Pedal Point at the Focus, the equation of the ellipse is
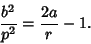 |
(44) |
To find the Radius of Curvature, return to the parametric coordinates centered at the center of the
ellipse and compute the first and second derivatives,
Therefore,
Similarly, the unit Tangent Vector is given by
![\begin{displaymath}
\hat{\bf T} = \left[{\matrix{-a\sin t\cr b\cos t\cr}}\right] {1\over \sqrt{a^2\sin ^2t+b^2\cos ^2t}}.
\end{displaymath}](e_534.gif) |
(50) |
The Arc Length of the ellipse can be computed using
where  is an incomplete Elliptic Integral of the Second Kind. Again, note that
is an incomplete Elliptic Integral of the Second Kind. Again, note that 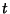 is a parameter which does not
have a direct interpretation in terms of an Angle. However, the relationship between the polar angle from the
ellipse center
is a parameter which does not
have a direct interpretation in terms of an Angle. However, the relationship between the polar angle from the
ellipse center 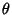 and the parameter
and the parameter 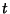 follows from
follows from
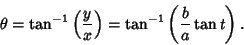 |
(52) |
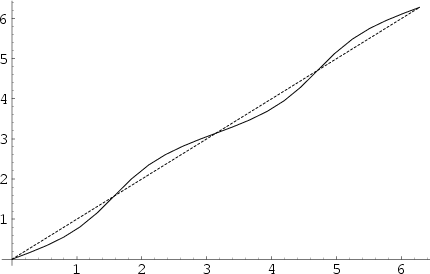
This function is illustrated above with 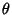 shown as the solid curve and
shown as the solid curve and 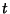 as the dashed, with
as the dashed, with 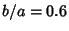 . Care must be
taken to make sure that the correct branch of the Inverse Tangent function is used. As can be seen,
. Care must be
taken to make sure that the correct branch of the Inverse Tangent function is used. As can be seen, 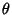 weaves back
and forth around
weaves back
and forth around 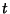 , with crossings occurring at multiples of
, with crossings occurring at multiples of 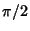 .
.
The Curvature and Tangential Angle of the ellipse are given by
The entire Perimeter 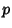 of the ellipse is given by setting
of the ellipse is given by setting  (corresponding to
(corresponding to 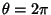 ), which is equivalent
to four times the length of one of the ellipse's Quadrants,
), which is equivalent
to four times the length of one of the ellipse's Quadrants,
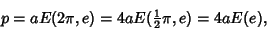 |
(55) |
where 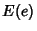 is a complete Elliptic Integral of the Second Kind with Modulus
is a complete Elliptic Integral of the Second Kind with Modulus 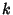 .
The Perimeter can be computed numerically by the rapidly converging Gauss-Kummer Series
.
The Perimeter can be computed numerically by the rapidly converging Gauss-Kummer Series
where
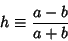 |
(57) |
and 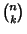 is a Binomial Coefficient. Approximations to the Perimeter include
is a Binomial Coefficient. Approximations to the Perimeter include
where the last two are due to Ramanujan (1913-14),
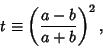 |
(61) |
and (60) is accurate to within
 .
.
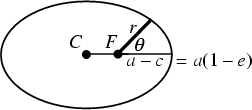
The maximum and minimum distances from the Focus are called the Apoapsis and Periapsis, and are
given by
The Area of an ellipse may be found by direct Integration
The Area can also be computed more simply by making the change of coordinates
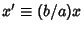 and
and 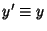 from the
elliptical region
from the
elliptical region 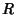 to the new region
to the new region 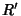 . Then the equation becomes
. Then the equation becomes
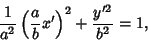 |
(65) |
or 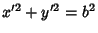 , so
, so 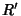 is a Circle of Radius
is a Circle of Radius  . Since
. Since
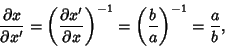 |
(66) |
the Jacobian is
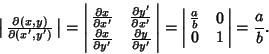 |
(67) |
The Area is therefore
as before. The Area of an arbitrary ellipse given by the Quadratic Equation
 |
(69) |
is
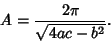 |
(70) |
The Area of an Ellipse with semiaxes  and
and  with respect to a
Pedal Point
with respect to a
Pedal Point  is
is
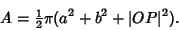 |
(71) |
The ellipse Inscribed in a given Triangle and tangent at its Midpoints is called the
Midpoint Ellipse. The Locus of the centers of the ellipses Inscribed in a Triangle is the interior
of the Medial Triangle. Newton  gave the solution to inscribing an ellipse in a convex Quadrilateral
(Dörrie 1965, p. 217). The centers of the ellipses Inscribed in a Quadrilateral all lie on the straight line
segment joining the Midpoints of the Diagonals (Chakerian 1979,
pp. 136-139).
gave the solution to inscribing an ellipse in a convex Quadrilateral
(Dörrie 1965, p. 217). The centers of the ellipses Inscribed in a Quadrilateral all lie on the straight line
segment joining the Midpoints of the Diagonals (Chakerian 1979,
pp. 136-139).
The Area of an ellipse with Barycentric Coordinates
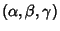 Inscribed in a
Triangle of unit Area is
Inscribed in a
Triangle of unit Area is
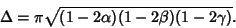 |
(72) |
(Chakerian 1979, pp. 142-145).
The Locus of the apex of a variable Cone containing an ellipse fixed in 3-space is a Hyperbola through the
Foci of the ellipse. In addition, the Locus of the apex of a Cone containing that
Hyperbola is the original ellipse. Furthermore, the Eccentricities of the ellipse and
Hyperbola are reciprocals. The Locus of centers of a Pappus Chain of Circles is an
ellipse. Surprisingly, the locus of the end of a garage door mounted on rollers along a vertical track but extending beyond
the track is a quadrant of an ellipse (the envelopes of positions is an Astroid).
See also Circle, Conic Section, Eccentric Anomaly, Eccentricity, Elliptic Cone,
Elliptic Curve, Elliptic Cylinder, Hyperbola, Midpoint Ellipse, Parabola,
Paraboloid, Quadratic Curve, Reflection Property, Salmon's Theorem, Steiner's
Ellipse
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 126 and 198-199, 1987.
Casey, J. ``The Ellipse.'' Ch. 6 in
A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing
an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., pp. 201-249, 1893.
Chakerian, G. D. ``A Distorted View of Geometry.'' Ch. 7 in Mathematical Plums
(Ed. R. Honsberger). Washington, DC: Math. Assoc. Amer., 1979.
Courant, R. and Robbins, H. What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, p. 75, 1996.
Dörrie, H. 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, 1965.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 72-78, 1972.
Lee, X. ``Ellipse.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/Ellipse_dir/ellipse.html.
Lockwood, E. H. ``The Ellipse.'' Ch. 2 in A Book of Curves. Cambridge, England: Cambridge University Press,
pp. 13-24, 1967.
MacTutor History of Mathematics Archive. ``Ellipse.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Ellipse.html.
Ramanujan, S. ``Modular Equations and Approximations to 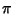 .'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
.'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() and
and ![]() from two fixed points
from two fixed points ![]() and
and ![]() (the Foci) separated by a distance of
(the Foci) separated by a distance of ![]() is a given Positive
constant
is a given Positive
constant ![]() (left figure). This results in the two-center Bipolar Coordinate equation
(left figure). This results in the two-center Bipolar Coordinate equation
![]() and named by Apollonius.
and named by Apollonius. ![]() The
Focus and Directrix of an ellipse were considered by Pappus. In 1602,
Kepler
The
Focus and Directrix of an ellipse were considered by Pappus. In 1602,
Kepler ![]() believed that the orbit of Mars
believed that the orbit of Mars ![]() was Oval; he later discovered that it was an ellipse
with the Sun
was Oval; he later discovered that it was an ellipse
with the Sun ![]() at one Focus. In fact, Kepler introduced the word ``Focus'' and published his
discovery in 1609. In 1705 Halley
at one Focus. In fact, Kepler introduced the word ``Focus'' and published his
discovery in 1609. In 1705 Halley ![]() showed that the comet
showed that the comet ![]() which is now named after him moved in an
elliptical orbit around the Sun (MacTutor Archive).
which is now named after him moved in an
elliptical orbit around the Sun (MacTutor Archive).
![]() and
and ![]() are at
are at ![]() and
and ![]() . In Cartesian Coordinates,
. In Cartesian Coordinates,
![]() ,
, ![]() ), equation (9) becomes
), equation (9) becomes
![]() and
and ![]() coordinates having different scalings,
coordinates having different scalings,
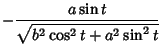

![]() to the x-Axis, the
parametric equations are
to the x-Axis, the
parametric equations are
![$\displaystyle \left[\begin{array}{cc}\cos\theta & \sin\theta\\ -\sin\theta & \...
...ta\end{array}\right] \left[\begin{array}{c}a\cos t\\ b\sin t\end{array}\right]$](e_477.gif)
![$\displaystyle \left[\begin{array}{c}a\cos\theta\cos t+b\sin\theta\sin t\\ -a\sin\theta\cos t+b\cos\theta\sin t\end{array}\right].$](e_478.gif)

![]() measured from the center of the ellipse is
called the Eccentric Angle. Writing
measured from the center of the ellipse is
called the Eccentric Angle. Writing ![]() for the distance of a point from the ellipse center, the equation in
Polar Coordinates is just given by the usual
for the distance of a point from the ellipse center, the equation in
Polar Coordinates is just given by the usual
![]() and
and ![]() are measured from a Focus instead of from the center, as they commonly are in
orbital mechanics,
are measured from a Focus instead of from the center, as they commonly are in
orbital mechanics, ![]() then the equations of the ellipse are
then the equations of the ellipse are
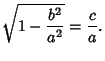
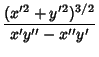

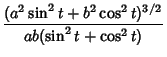
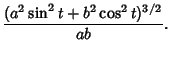


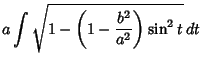
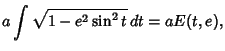
![]() shown as the solid curve and
shown as the solid curve and ![]() as the dashed, with
as the dashed, with ![]() . Care must be
taken to make sure that the correct branch of the Inverse Tangent function is used. As can be seen,
. Care must be
taken to make sure that the correct branch of the Inverse Tangent function is used. As can be seen, ![]() weaves back
and forth around
weaves back
and forth around ![]() , with crossings occurring at multiples of
, with crossings occurring at multiples of ![]() .
.

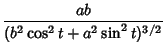
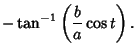
![]() of the ellipse is given by setting
of the ellipse is given by setting ![]() (corresponding to
(corresponding to ![]() ), which is equivalent
to four times the length of one of the ellipse's Quadrants,
), which is equivalent
to four times the length of one of the ellipse's Quadrants,
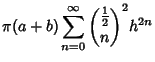

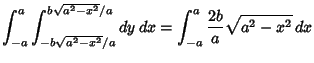
![$\displaystyle {2b\over a}\left\{{{1\over 2} \left[{x\sqrt{a^2-x^2}+a^2\sin^{-1}\left({x\over \vert a\vert}\right)}\right]}\right\}^a_{x=-a}$](e_569.gif)
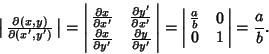

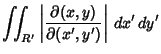

![]() gave the solution to inscribing an ellipse in a convex Quadrilateral
(Dörrie 1965, p. 217). The centers of the ellipses Inscribed in a Quadrilateral all lie on the straight line
segment joining the Midpoints of the Diagonals (Chakerian 1979,
pp. 136-139).
gave the solution to inscribing an ellipse in a convex Quadrilateral
(Dörrie 1965, p. 217). The centers of the ellipses Inscribed in a Quadrilateral all lie on the straight line
segment joining the Midpoints of the Diagonals (Chakerian 1979,
pp. 136-139).
![]() Inscribed in a
Triangle of unit Area is
Inscribed in a
Triangle of unit Area is
![]() .'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
.'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.