|
|
|
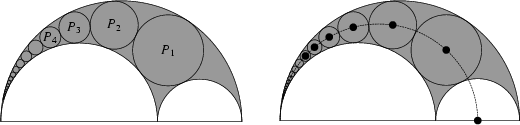
In the Arbelos, construct a chain of Tangent Circles starting with the Circle
Tangent to the two small interior semicircles and the large exterior one. Then the distance from the center of the first
Inscribed Circle to the bottom line is twice the Circle's Radius, from the second
Circle is four times the Radius, and for the ![]() th Circle is
th Circle is ![]() times the Radius. The centers of
the Circles lie on an Ellipse, and the Diameter of the
times the Radius. The centers of
the Circles lie on an Ellipse, and the Diameter of the ![]() th Circle
th Circle ![]() is (
is (![]() )th Perpendicular distance to the base of the Semicircle. This result was known to
Pappus,
)th Perpendicular distance to the base of the Semicircle. This result was known to
Pappus, ![]() who referred to it as an ancient theorem (Hood 1961, Cadwell 1966, Gardner 1979, Bankoff 1981). The
simplest proof is via Inversive Geometry.
who referred to it as an ancient theorem (Hood 1961, Cadwell 1966, Gardner 1979, Bankoff 1981). The
simplest proof is via Inversive Geometry.
If ![]() , then the radius of the
, then the radius of the ![]() th circle in the pappus chain is
th circle in the pappus chain is
If ![]() divides
divides ![]() in the Golden Ratio
in the Golden Ratio ![]() , then the circles in the chain satisfy a number of other special properties
(Bankoff 1955).
, then the circles in the chain satisfy a number of other special properties
(Bankoff 1955).
See also Arbelos, Coxeter's Loxodromic Sequence of Tangent Circles, Soddy Circles, Steiner Chain
References
Bankoff, L. ``The Golden Arbelos.'' Scripta Math. 21, 70-76, 1955.
Bankoff, L. ``Are the Twin Circles of Archimedes Really Twins?'' Math. Mag. 47, 214-218, 1974.
Bankoff, L. ``How Did Pappus Do It?'' In The Mathematical Gardner (Ed. D. Klarner). Boston, MA: Prindle, Weber,
and Schmidt, pp. 112-118, 1981.
Gaba, M. G. ``On a Generalization of the Arbelos.'' Amer. Math. Monthly 47, 19-24, 1940.
Gardner, M. ``Mathematical Games: The Diverse Pleasures of Circles that Are Tangent to One Another.'' Sci. Amer. 240,
18-28, Jan. 1979.
Hood, R. T. ``A Chain of Circles.'' Math. Teacher 54, 134-137, 1961.
Johnson, R. A. Advanced Euclidean Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle.
Boston, MA: Houghton Mifflin, p. 117, 1929.
|
|
|
© 1996-9 Eric W. Weisstein