|
|
|

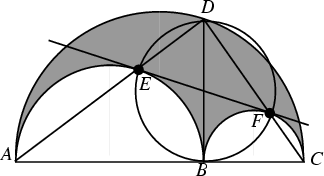
The term ``arbelos'' means Shoemaker's Knife in Greek, and this term is applied to the shaded Area in the above
figure which resembles the blade of a knife used by ancient cobblers (Gardner 1979). Archimedes ![]() himself is believed
to have been the first mathematician to study the mathematical properties of this figure. The position of the central notch is
arbitrary and can be located anywhere along the Diameter.
himself is believed
to have been the first mathematician to study the mathematical properties of this figure. The position of the central notch is
arbitrary and can be located anywhere along the Diameter.
The arbelos satisfies a number of unexpected identities (Gardner 1979).

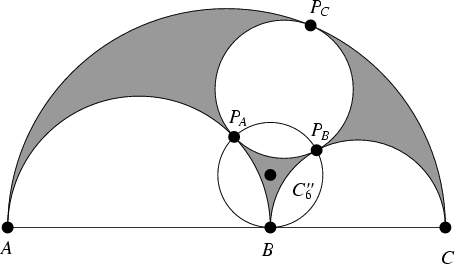
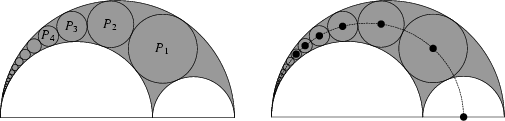
See also Archimedes' Circles, Bankoff Circle, Coxeter's Loxodromic Sequence of Tangent Circles, Golden Ratio, Inversion, Pappus Chain, Steiner Chain
References
Bankoff, L. ``The Fibonacci Arbelos.'' Scripta Math. 20, 218, 1954.
Bankoff, L. ``The Golden Arbelos.'' Scripta Math. 21, 70-76, 1955.
Bankoff, L. ``Are the Twin Circles of Archimedes Really Twins?'' Math. Mag. 47, 214-218, 1974.
Bankoff, L. ``How Did Pappus Do It?'' In The Mathematical Gardner (Ed. D. Klarner). Boston, MA: Prindle, Weber,
and Schmidt, pp. 112-118, 1981.
Bankoff, L. ``The Marvelous Arbelos.'' In The Lighter Side of Mathematics
(Ed. R. K. Guy and R. E. Woodrow). Washington, DC: Math. Assoc. Amer., 1994.
Cadwell, J. H. Topics in Recreational Mathematics. Cambridge, England: Cambridge University Press, 1966.
Gaba, M. G. ``On a Generalization of the Arbelos.'' Amer. Math. Monthly 47, 19-24, 1940.
Gardner, M. ``Mathematical Games: The Diverse Pleasures of Circles that Are Tangent to One Another.'' Sci. Amer. 240,
18-28, Jan. 1979.
Heath, T. L. The Works of Archimedes with the Method of Archimedes. New York: Dover, 1953.
Hood, R. T. ``A Chain of Circles.'' Math. Teacher 54, 134-137, 1961.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle.
Boston, MA: Houghton Mifflin, pp. 116-117, 1929.
Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 54-55, 1990.
|
|
|
© 1996-9 Eric W. Weisstein