|
|
|
Given a set
![]() of
of ![]() equations in
equations in ![]() variables
variables ![]() , ...,
, ..., ![]() , written explicitly as
, written explicitly as
![\begin{displaymath}
{\bf y}\equiv\left[{\matrix{f_1({\bf x})\cr f_2({\bf x})\cr \vdots\cr f_n({\bf x})\cr}}\right],
\end{displaymath}](j_446.gif) |
(1) |
 |
(2) |
![\begin{displaymath}
{\hbox{\sf J}}(x_1,\dots,x_n) = \left[{\matrix{
{\partial y...
...n\over\partial x_n}\cr}}\right].
\hrule width 0pt height 6.6pt
\end{displaymath}](j_448.gif) |
(3) |
| (4) |
Taking the differential
| (5) |
| (6) |
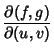 |
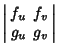 |
(7) | |
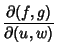 |
 |
(8) |
For the case of ![]() variables, the Jacobian takes the special form
variables, the Jacobian takes the special form
| (9) |
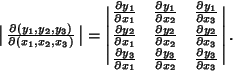 |
(10) |
See also Change of Variables Theorem, Curvilinear Coordinates, Implicit Function Theorem
References
Kaplan, W. Advanced Calculus, 3rd ed. Reading, MA: Addison-Wesley, pp. 98-99, 123, and 238-245, 1984.
Simon, C. P. and Blume, L. E. Mathematics for Economists. New York: W. W. Norton, 1994.
|
|
|
© 1996-9 Eric W. Weisstein