Bipolar coordinates are a 2-D system of coordinates. There are two commonly defined types of bipolar coordinates, the first of
which is defined by
where
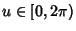 ,
,
 . The following identities show that curves of constant
. The following identities show that curves of constant 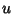 and
and 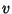 are
Circles in
are
Circles in 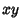 -space.
-space.
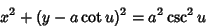 |
(3) |
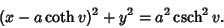 |
(4) |
The Scale Factors are
The Laplacian is
Laplace's Equation is separable.
Two-center bipolar coordinates are two coordinates giving the distances from two fixed centers 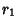 and
and 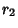 , sometimes
denoted
, sometimes
denoted 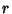 and
and 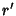 . For two-center bipolar coordinates with centers at
. For two-center bipolar coordinates with centers at 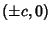 ,
,
Combining (8) and (9) gives
 |
(10) |
Solving for Cartesian Coordinates 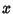 and
and  gives
gives
Solving for Polar Coordinates gives
References
Lockwood, E. H. ``Bipolar Coordinates.'' Ch. 25 in A Book of Curves. Cambridge, England: Cambridge University Press,
pp. 186-190, 1967.
© 1996-9 Eric W. Weisstein
1999-05-26
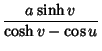
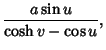
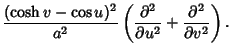
![]() and
and ![]() , sometimes
denoted
, sometimes
denoted ![]() and
and ![]() . For two-center bipolar coordinates with centers at
. For two-center bipolar coordinates with centers at ![]() ,
,
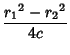
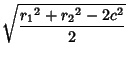
![$\displaystyle \tan^{-1}\left[{\sqrt{{8c^2({r_1}^2+{r_2}^2-2c^2)\over {r_1}^2-{r_2}^2}-1}\,}\right].$](b_1489.gif)