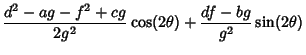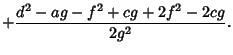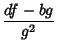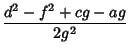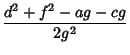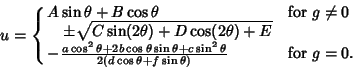The general 2-variable quadratic equation can be written
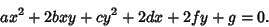 |
(1) |
Define the following quantities:
Then the quadratics are classified into the types summarized in the following table (Beyer 1987). The real (nondegenerate)
quadratics (the Ellipse, Hyperbola, and Parabola) correspond to the curves which can be created by the
intersection of a Plane with a (two-Nappes) Cone, and are therefore known as Conic
Sections.
| Curve |
 |
 |
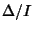 |
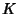 |
| Coincident Lines |
0 |
0 |
|
0 |
| Ellipse (Imaginary) |
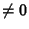 |
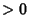 |
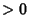 |
|
| Ellipse (Real) |
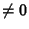 |
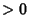 |
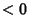 |
|
| Hyperbola |
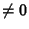 |
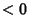 |
|
|
| Intersecting Lines (Imaginary) |
0 |
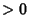 |
|
|
| Intersecting Lines (Real) |
0 |
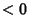 |
|
|
| Parabola |
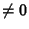 |
0 |
|
|
| Parallel Lines (Imaginary) |
0 |
0 |
|
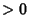 |
| Parallel Lines (Real) |
0 |
0 |
|
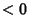 |
It is always possible to eliminate the  cross term by a suitable Rotation of the axes. To see this, consider
rotation by an arbitrary angle
cross term by a suitable Rotation of the axes. To see this, consider
rotation by an arbitrary angle  . The Rotation Matrix is
. The Rotation Matrix is
so
Plugging these into (1) gives
Rewriting,
Grouping terms,
Comparing the Coefficients with (1) gives an equation of the form
 |
(15) |
where the new Coefficients are
 |
 |
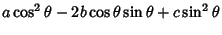 |
(16) |
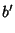 |
 |
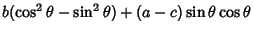 |
(17) |
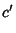 |
 |
 |
(18) |
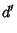 |
 |
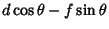 |
(19) |
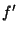 |
 |
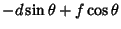 |
(20) |
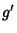 |
 |
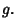 |
(21) |
The cross term 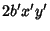 can therefore be made to vanish by setting
can therefore be made to vanish by setting
For 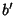 to be zero, it must be true that
to be zero, it must be true that
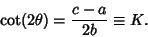 |
(23) |
The other components are then given with the aid of the identity
![\begin{displaymath}
\cos[\cot^{-1}(x)] = {x\over\sqrt{1+x^2}}
\end{displaymath}](q_193.gif) |
(24) |
by defining
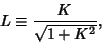 |
(25) |
so
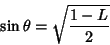 |
(26) |
 |
(27) |
Rotating by an angle
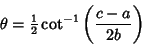 |
(28) |
therefore transforms (1) into
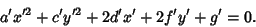 |
(29) |
Completing the Square,
 |
(30) |
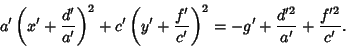 |
(31) |
Defining
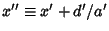 ,
,
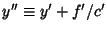 , and
, and
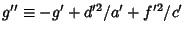 gives
gives
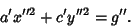 |
(32) |
If 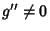 , then divide both sides by
, then divide both sides by  .
Defining
.
Defining
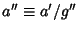 and
and
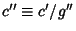 then gives
then gives
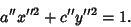 |
(33) |
Therefore, in an appropriate coordinate system, the general Conic Section
can be written (dropping the primes) as
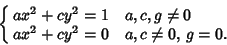 |
(34) |
Consider an equation of the form
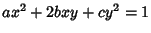 where
where  .
Re-express this using
.
Re-express this using  and
and  in the form
in the form
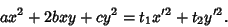 |
(35) |
Therefore, rotate the Coordinate System
![\begin{displaymath}
\left[{\matrix{x'\cr y'\cr}}\right] =\left[{\matrix{\cos \th...
...& \cos \theta \cr}}\right]
\left[{\matrix{x\cr y\cr}}\right],
\end{displaymath}](q_216.gif) |
(36) |
so
and
Therefore,
From (41) and (42),
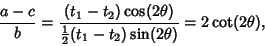 |
(43) |
the same angle as before. But
so
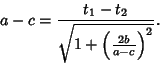 |
(45) |
Rewriting and copying (41),
Adding (46) and (47) gives
Note that these Roots can also be found from
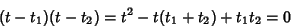 |
(50) |
The original problem is therefore equivalent to looking for a solution to
![\begin{displaymath}
\left[{\matrix{a & b\cr b & c\cr}}\right]\left[{\matrix{x\cr y\cr}}\right] =t\left[{\matrix{x\cr y\cr}}\right]
\end{displaymath}](q_252.gif) |
(52) |
![\begin{displaymath}
\left[{\matrix{ax & bx\cr by & cy\cr}}\right]\left[{\matrix{x\cr y\cr}}\right]=t\left[{\matrix{x^2\cr y^2\cr}}\right],
\end{displaymath}](q_253.gif) |
(53) |
which gives the simultaneous equations
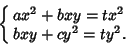 |
(54) |
Let  be any point
be any point  with old coordinates and
with old coordinates and 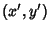 be its new
coordinates. Then
be its new
coordinates. Then
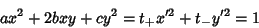 |
(55) |
and
If 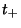 and
and 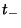 are both
are both 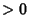 , the curve is an Ellipse. If
, the curve is an Ellipse. If 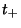 and
and 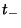 are both
are both 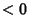 , the curve is empty.
If
, the curve is empty.
If 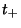 and
and 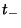 have opposite Signs, the curve is a Hyperbola. If either is 0, the curve is a
Parabola.
have opposite Signs, the curve is a Hyperbola. If either is 0, the curve is a
Parabola.
To find the general form of a quadratic curve in Polar Coordinates (as given, for example, in Moulton 1970), plug
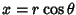 and
and  into (1) to obtain
into (1) to obtain
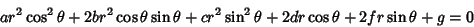 |
(58) |
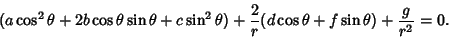 |
(59) |
Define 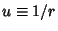 . For
. For 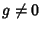 ,we can divide through by
,we can divide through by 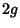 ,
,
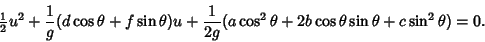 |
(60) |
Applying the Quadratic Formula gives
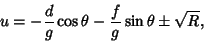 |
(61) |
where
Using the trigonometric identities
it follows that
Defining
then gives the equation
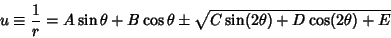 |
(71) |
(Moulton 1970). If 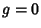 , then (0) becomes instead
, then (0) becomes instead
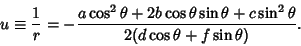 |
(72) |
Therefore, the general form of a quadratic curve in polar coordinates is given by
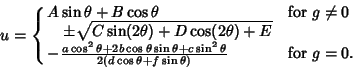 |
(73) |
See also Conic Section, Discriminant (Quadratic Curve), Elliptic Curve
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 200-201, 1987.
Casey, J. ``The General Equation of the Second Degree.'' Ch. 4 in
A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing
an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., pp. 151-172, 1893.
Moulton, F. R. ``Law of Force in Binary Stars'' and ``Geometrical Interpretation of the Second Law.'' §58 and 59 in
An Introduction to Celestial Mechanics, 2nd rev. ed.
New York: Dover, pp. 86-89, 1970.
© 1996-9 Eric W. Weisstein
1999-05-25

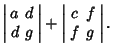
![]() cross term by a suitable Rotation of the axes. To see this, consider
rotation by an arbitrary angle
cross term by a suitable Rotation of the axes. To see this, consider
rotation by an arbitrary angle ![]() . The Rotation Matrix is
. The Rotation Matrix is
![$\displaystyle \left[\begin{array}{cc}\cos\theta & \sin\theta\\ -\sin\theta & \cos\theta\end{array}\right]\left[\begin{array}{c}x'\\ y'\end{array}\right]$](q_152.gif)
![$\displaystyle \left[\begin{array}{c}x'\cos\theta +y'\sin\theta\\ -x'\sin\theta +y'\cos\theta\end{array}\right],$](q_153.gif)
![]() where
where ![]() .
Re-express this using
.
Re-express this using ![]() and
and ![]() in the form
in the form
![$\displaystyle \cos \left[{\cot^{-1}\left({a-c\over 2b}\right)}\right]$](q_235.gif)
![$\displaystyle \cos\left[{\tan^{-1}\left({2b\over a-c}\right)}\right]$](q_236.gif)

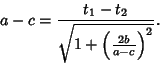
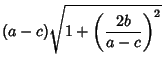
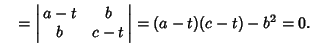
![]() be any point
be any point ![]() with old coordinates and
with old coordinates and ![]() be its new
coordinates. Then
be its new
coordinates. Then
![$\displaystyle {\hat {\bf X}}_+\cdot \left[\begin{array}{c}x\\ y\end{array}\right]$](q_259.gif)
![$\displaystyle {\hat {\bf X}}_-\cdot \left[\begin{array}{c}x\\ y\end{array}\right].$](q_261.gif)
![]() and
and ![]() into (1) to obtain
into (1) to obtain
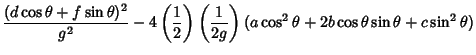
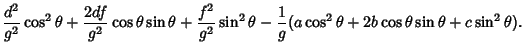
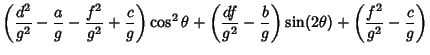
![$\displaystyle {\textstyle{1\over 2}}[1+\cos(2\theta)]{d^2-ag-f^2+cg\over g^2}+\sin(2\theta)\left({df-bg\over g^2}\right)+{f^2-cg\over g^2}$](q_281.gif)