The straight line on which all Points at Infinity lie. The line at infinity is given in
terms of Trilinear Coordinates by
which follows from the fact that a Real Triangle will have Positive Area, and
therefore that
Instead of the three reflected segments concurring for the Isogonal Conjugate of a point 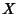 on the
Circumcircle of a Triangle, they become parallel (and can be considered to meet at infinity). As
on the
Circumcircle of a Triangle, they become parallel (and can be considered to meet at infinity). As 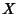 varies around
the Circumcircle,
varies around
the Circumcircle, 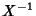 varies through a line called the line at infinity. Every line is Perpendicular to the
line at infinity.
varies through a line called the line at infinity. Every line is Perpendicular to the
line at infinity.
See also Point at Infinity
© 1996-9 Eric W. Weisstein
1999-05-25