|
|
|
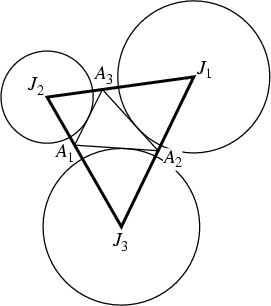
The Triangle
![]() with Vertices corresponding to the Excenters of a given
Triangle
with Vertices corresponding to the Excenters of a given
Triangle ![]() , also called the Tritangent Triangle.
, also called the Tritangent Triangle.
Beginning with an arbitrary Triangle ![]() , find the excentral triangle
, find the excentral triangle ![]() . Then find the excentral triangle
. Then find the excentral triangle ![]() of that
Triangle, and so on. Then the resulting Triangle
of that
Triangle, and so on. Then the resulting Triangle ![]() approaches an Equilateral Triangle.
approaches an Equilateral Triangle.
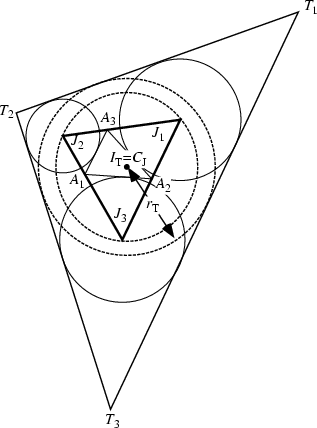
Call ![]() the Triangle tangent externally to the Excircles of
the Triangle tangent externally to the Excircles of ![]() . Then the Incenter
. Then the Incenter
![]() of
of ![]() coincides with the Circumcenter
coincides with the Circumcenter ![]() of Triangle
of Triangle
![]() , where
, where ![]() are the
Excenters of
are the
Excenters of ![]() . The Inradius
. The Inradius ![]() of the Incircle of
of the Incircle of ![]() is
is
See also Excenter, Excenter-Excenter Circle, Excircle, Mittenpunkt
References
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, 1929.