|
|
|
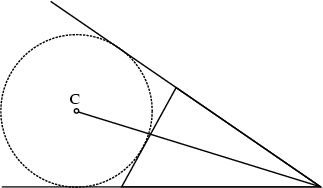
Given a Triangle, extend two nonadjacent sides. The Circle tangent to these two lines and to the other
side of the Triangle is called an Escribed Circle, or excircle. The Center ![]() of the excircle is
called the Excenter and lies on the external Angle Bisector of the opposite Angle. Every
Triangle has three excircles, and the Trilinear Coordinates of the Excenters are
of the excircle is
called the Excenter and lies on the external Angle Bisector of the opposite Angle. Every
Triangle has three excircles, and the Trilinear Coordinates of the Excenters are
![]() ,
, ![]() , and
, and ![]() . The Radius
. The Radius ![]() of the excircle
of the excircle ![]() is called its Exradius.
is called its Exradius.
Given a Triangle with Inradius ![]() , let
, let ![]() be the Altitudes of the excircles, and
be the Altitudes of the excircles, and
![]() their Radii (the Exradii). Then
their Radii (the Exradii). Then
See also Excenter, Excenter-Excenter Circle, Excentral Triangle, Feuerbach's Theorem, Nagel Point, Triangle Transformation Principle
References
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 11-13,
1967.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, pp. 176-177 and 182-194, 1929.