|
|
|
The region between two Concentric circles of different Radii is called an Annulus.
Given two concentric circles with Radii ![]() and
and ![]() , what is the probability that a chord chosen at
random from the outer circle will cut across the inner circle? Depending on how the ``random'' Chord is chosen,
1/2, 1/3, or 1/4 could all be correct answers.
, what is the probability that a chord chosen at
random from the outer circle will cut across the inner circle? Depending on how the ``random'' Chord is chosen,
1/2, 1/3, or 1/4 could all be correct answers.
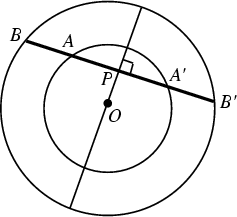
Given an arbitrary Chord ![]() to the larger of two concentric Circles centered on
to the larger of two concentric Circles centered on ![]() , the
distance between inner and outer intersections is equal on both sides
, the
distance between inner and outer intersections is equal on both sides ![]() . To prove this, take the
Perpendicular to
. To prove this, take the
Perpendicular to ![]() passing through
passing through ![]() and crossing at
and crossing at ![]() . By symmetry, it must be true that
. By symmetry, it must be true that ![]() and
and ![]() are equal. Similarly,
are equal. Similarly, ![]() and
and ![]() must be equal. Therefore,
must be equal. Therefore, ![]() equals
equals
![]() . Incidentally, this
is also true for Homeoids, but the proof is nontrivial.
. Incidentally, this
is also true for Homeoids, but the proof is nontrivial.
See also Annulus