|
|
|
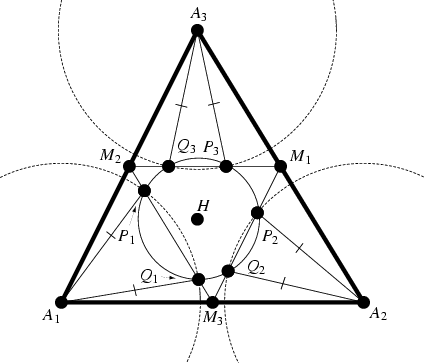
Draw a Circle with center ![]() which cuts the lines
which cuts the lines ![]() ,
, ![]() , and
, and ![]() (where
(where ![]() are the
Midpoints) at
are the
Midpoints) at ![]() ,
, ![]() ;
; ![]() ,
, ![]() ; and
; and ![]() ,
, ![]() respectively, then
respectively, then
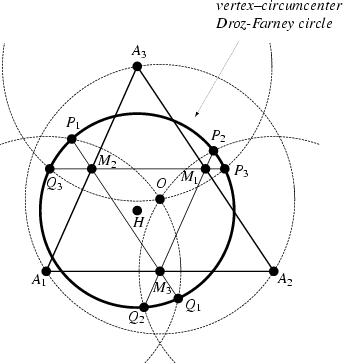
If the circles equal to the Circumcircle are drawn about the Vertices of a triangle, they
cut the lines joining midpoints of the adjacent sides in points of a Circle ![]() with center
with center ![]() and Radius
and Radius
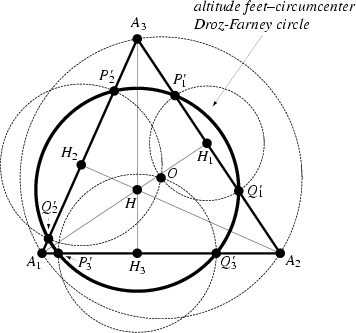
It is equivalent to the circle obtained by drawing circles with centers at the feet
of the altitudes and passing through the Circumcenter. These circles cut the corresponding sides in six points on a
circle ![]() whose center is
whose center is ![]() .
.
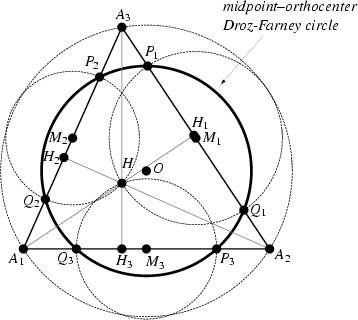
Furthermore, the circles about the midpoints of the sides and passing though ![]() cut the sides in six points lying on another
equivalent circle
cut the sides in six points lying on another
equivalent circle ![]() whose center is
whose center is ![]() . In summary, the second Droz-Farny circle passes through 12 notable points, two
on each of the sides and two on each of the lines joining midpoints of the sides.
. In summary, the second Droz-Farny circle passes through 12 notable points, two
on each of the sides and two on each of the lines joining midpoints of the sides.
References
Goormaghtigh, R. ``Droz-Farny's Theorem.'' Scripta Math. 16, 268-271, 1950.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, pp. 256-258, 1929.
|
|
|
© 1996-9 Eric W. Weisstein