|
|
|
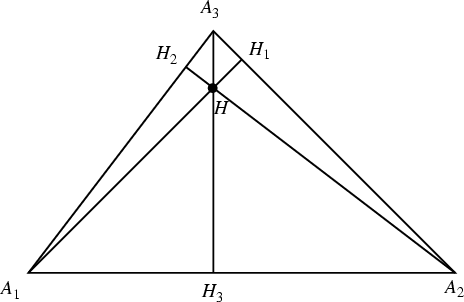
The intersection ![]() of the three Altitudes of a Triangle
is called the orthocenter. Its Trilinear Coordinates are
of the three Altitudes of a Triangle
is called the orthocenter. Its Trilinear Coordinates are
| (1) |
| (2) |

The Circumcenter ![]() and orthocenter
and orthocenter ![]() are Isogonal Conjugate points.
The orthocenter lies on the Euler Line.
are Isogonal Conjugate points.
The orthocenter lies on the Euler Line.
| (3) |
| (4) |
| (5) |
Any Hyperbola circumscribed on a Triangle and passing through the orthocenter is Rectangular, and has its center on the Nine-Point Circle (Falisse 1920, Vandeghen 1965).
See also Centroid (Triangle), Circumcenter, Euler Line, Incenter, Orthic Triangle, Orthocentric Coordinates, Orthocentric Quadrilateral, Orthocentric System, Polar Circle
References
Altshiller-Court, N. College Geometry: A Second Course in Plane Geometry for Colleges and Normal Schools, 2nd ed.
New York: Barnes and Noble, pp. 165-172, 1952.
Carr, G. S. Formulas and Theorems in Pure Mathematics, 2nd ed. New York: Chelsea, p. 622, 1970.
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 36-40, 1967.
Dixon, R. Mathographics. New York: Dover, p. 57, 1991.
Falisse, V. Cours de géométrie analytique plane. Brussels, Belgium: Office de Publicité, 1920.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, pp. 165-172 and 191, 1929.
Kimberling, C. ``Central Points and Central Lines in the Plane of a Triangle.'' Math. Mag. 67, 163-187, 1994.
Kimberling, C. ``Orthocenter.''
http://cedar.evansville.edu/~ck6/tcenters/class/orthocn.html.
Vandeghen, A. ``Some Remarks on the Isogonal and Cevian Transforms. Alignments of Remarkable Points of a Triangle.''
Amer. Math. Monthly 72, 1091-1094, 1965.
|
|
|
© 1996-9 Eric W. Weisstein