|
|
|
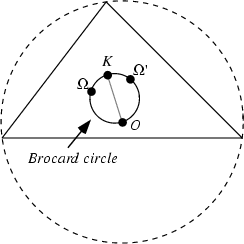
The Circle passing through the first and second Brocard Points ![]() and
and ![]() , the Lemoine
Point
, the Lemoine
Point ![]() , and the Circumcenter
, and the Circumcenter ![]() of a given Triangle. The Brocard Points
of a given Triangle. The Brocard Points ![]() and
and ![]() are symmetrical about the Line
are symmetrical about the Line
![]() , which is called the Brocard Line.
The Line Segment
, which is called the Brocard Line.
The Line Segment ![]() is called the Brocard Diameter, and it has length
is called the Brocard Diameter, and it has length
See also Brocard Angle, Brocard Diameter, Brocard Points
References
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, p. 272, 1929.