|
|
|
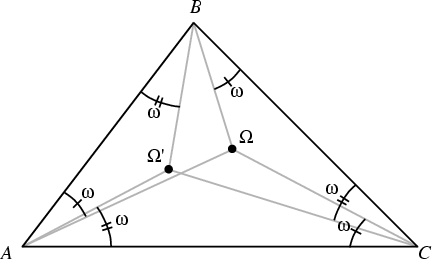
Define the first Brocard Point as the interior point ![]() of a Triangle for which the
Angles
of a Triangle for which the
Angles
![]() ,
,
![]() , and
, and
![]() are equal. Similarly, define the second
Brocard Point as the interior point
are equal. Similarly, define the second
Brocard Point as the interior point ![]() for which the Angles
for which the Angles
![]() ,
,
![]() , and
, and
![]() are equal. Then the Angles in both cases are equal, and this angle is
called the Brocard angle, denoted
are equal. Then the Angles in both cases are equal, and this angle is
called the Brocard angle, denoted ![]() .
.
The Brocard angle ![]() of a Triangle
of a Triangle ![]() is given by the formulas
is given by the formulas
| (1) | |||
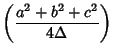 |
(2) | ||
| (3) | |||
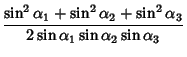 |
(4) | ||
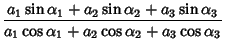 |
(5) | ||
| (6) | |||
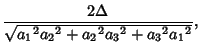 |
(7) |
If an Angle ![]() of a Triangle is given, the maximum possible Brocard angle is given by
of a Triangle is given, the maximum possible Brocard angle is given by
| (8) |
| (9) |
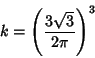 |
(10) |
| (11) |
See also Brocard Circle, Brocard Line, Equi-Brocard Center, Fermat Point, Isogonic Centers
References
Abi-Khuzam, F. ``Proof of Yff's Conjecture on the Brocard Angle of a Triangle.'' Elem. Math. 29, 141-142, 1974.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, pp. 263-286 and 289-294, 1929.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 28, 1983.
|
|
|
© 1996-9 Eric W. Weisstein