Lemoine Circle

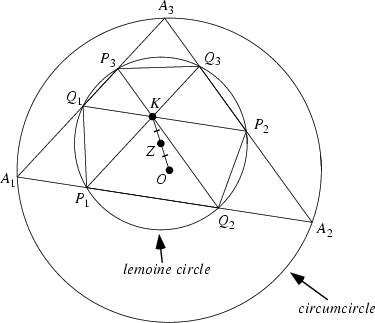
Also called the Triplicate-Ratio Circle. Draw lines through the Lemoine Point $K$ and parallel to the sides of the triangle. The points where the parallel lines intersect the sides then lie on a Circle known as the Lemoine circle. This circle has center at the Midpoint of $OK$, where $O$ is the Circumcenter. The circle has radius

$${\textstyle{1\over 2}}\sqrt{R^2+r_c^2}={\textstyle{1\over 2}}R\sec\omega,$$

where $R$ is the Circumradius, $r_c$ is the radius of the Cosine Circle, and $\omega$ is the Brocard Angle. The Lemoine circle divides any side into segments proportional to the squares of the sides

$$\overline{A_2P_2}:\overline{P_2Q_3}:\overline{Q_3A_3}={a_3}^2:{a_1}^2:{a_2}^2.$$

Furthermore, the chords cut from the sides by the Lemoine circle are proportional to the squares of the sides.

The Cosine Circle is sometimes called the second Lemoine circle.

See also Cosine Circle, Lemoine Line, Lemoine Point, Tucker Circles

References

Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 273-275, 1929.