Cosine Circle

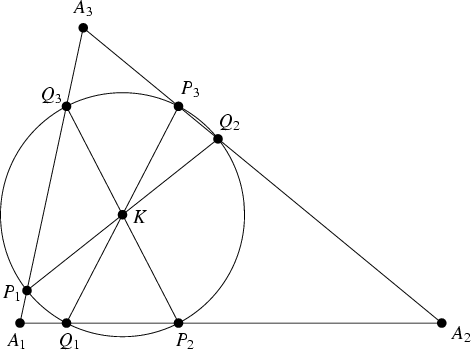
Also called the second Lemoine Circle. Draw lines through the Lemoine Point $K$ and Parallel to the sides of the Triangles. The points where the antiparallel lines intersect the sides then lie on a Circle known as the cosine circle with center at $K$. The Chords $P_2Q_3$, $P_3Q_1$, and $P_1Q_2$ are proportional to the Cosines of the Angles of $\Delta A_1A_2A_3$, giving the circle its name.

Triangles $P_1P_2P_3$ and $\Delta A_1A_2A_3$ are directly similar, and Triangles $\Delta Q_1Q_2Q_3$ and $A_1A_2A_3$ are similar. The Miquel Point of $\Delta P_1P_2P_3$ is at the Brocard Point $\Omega$ of $\Delta P_1P_2P_3$.

See also Brocard Points, Lemoine Circle, Miquel Point, Tucker Circles

References

Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 271-273, 1929.