According to Euler's Rotation Theorem, any Rotation may be described using three Angles. If
the Rotations are written in terms of Rotation Matrices B, C, and D,
then a general Rotation A can be written as
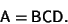 |
(1) |
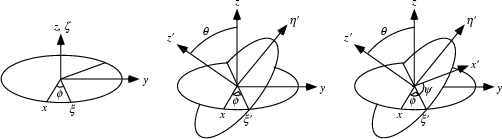
The three angles giving the three rotation matrices are called Euler angles. There are several conventions for Euler angles,
depending on the axes about which the rotations are carried out. Write the Matrix A as
![\begin{displaymath}
{\hbox{\sf A}}\equiv \left[{\matrix{
a_{11} & a_{12} & a_{13...
...21} & a_{22} & a_{23}\cr
a_{31} & a_{32} & a_{33}\cr}}\right].
\end{displaymath}](e_1911.gif) |
(2) |
In the so-called `` -convention,'' illustrated above,
-convention,'' illustrated above,
so
To obtain the components of the Angular Velocity
 in the body axes, note that for a Matrix
in the body axes, note that for a Matrix
![\begin{displaymath}
{\hbox{\sf A}}\equiv \left[{\matrix{{\bf A}_1 & {\bf A}_2 & {\bf A}_3\cr}}\right],
\end{displaymath}](e_1936.gif) |
(6) |
it is true that
Now, 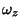 corresponds to rotation about the
corresponds to rotation about the  axis, so look at the
axis, so look at the 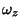 component of
component of
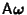 ,
,
![\begin{displaymath}
\boldsymbol{\omega}_\phi = {\bf A}_1\omega_z = \left[{\matri...
...theta\cr \cos\psi\sin\theta\cr\cos \theta\cr}}\right]\dot\phi.
\end{displaymath}](e_1942.gif) |
(9) |
The line of nodes corresponds to a rotation by 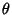 about the
about the 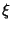 -axis, so look at the
-axis, so look at the 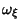 component of
component of
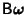 ,
,
![\begin{displaymath}
\boldsymbol{\omega}_\theta = {\bf B}_1\omega_\xi = {\bf B}_1...
...eft[{\matrix{\cos\psi\cr -\sin\psi\cr 0\cr}}\right]\dot\theta.
\end{displaymath}](e_1946.gif) |
(10) |
Similarly, to find rotation by  about the remaining axis, look at the
about the remaining axis, look at the 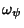 component of
component of
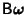 ,
,
![\begin{displaymath}
\boldsymbol{\omega}_\psi={\bf B}_3\omega_\psi = {\bf B}_3\dot\psi = \left[{\matrix{0\cr 0\cr 1\cr}}\right]\dot\psi.
\end{displaymath}](e_1949.gif) |
(11) |
Combining the pieces gives
![\begin{displaymath}
\boldsymbol{\omega}=\left[{\matrix{\sin\psi\sin\theta \dot\p...
...dot\phi-\sin\psi\cr
\cos\theta \dot\phi+\dot\psi.\cr}}\right]
\end{displaymath}](e_1950.gif) |
(12) |
For more details, see Goldstein (1980, p. 176) and Landau and Lifschitz (1976, p. 111).
The  -convention Euler angles are given in terms of the Cayley-Klein Parameters by
-convention Euler angles are given in terms of the Cayley-Klein Parameters by
In the ``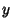 -convention,''
-convention,''
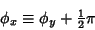 |
(16) |
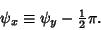 |
(17) |
Therefore,
 |
(18) |
 |
(19) |
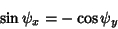 |
(20) |
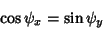 |
(21) |
and A is given by
In the ``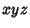 '' (pitch-roll-yaw) convention,
'' (pitch-roll-yaw) convention, 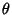 is pitch,
is pitch, 
 is
roll,
is
roll,  and
and  is yaw.
is yaw. 
and A is given by
A set of parameters sometimes used instead of angles are the Euler Parameters 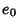 ,
, 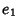 ,
, 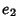 and
and 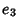 ,
defined by
,
defined by
Using Euler Parameters (which are Quaternions), an arbitrary Rotation Matrix can be
described by
(Goldstein 1960, p. 153).
If the coordinates of two pairs of  points
points 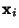 and
and 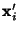 are known, one rotated with respect to the other,
then the Euler rotation matrix can be obtained in a straightforward manner using Least Squares Fitting. Write the
points as arrays of vectors, so
are known, one rotated with respect to the other,
then the Euler rotation matrix can be obtained in a straightforward manner using Least Squares Fitting. Write the
points as arrays of vectors, so
![\begin{displaymath}
\left[{\matrix{{\bf x}_1' & \cdots & {\bf x}_n'\cr}}\right] ...
... A}}\left[{\matrix{{\bf x}_1 & \cdots & {\bf x}_n\cr}}\right].
\end{displaymath}](e_2000.gif) |
(29) |
Writing the arrays of vectors as matrices gives
 |
(30) |
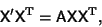 |
(31) |
and solving for
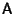 gives
gives
 |
(32) |
However, we want the angles 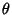 ,
,  , and
, and  , not their combinations contained in the Matrix
, not their combinations contained in the Matrix
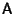 . Therefore, write the
. Therefore, write the 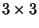 Matrix
Matrix
![\begin{displaymath}
{\hbox{\sf A}}=\left[{\matrix{
f_1(\theta,\phi,\psi) & f_2(\...
...i) & f_7(\theta,\phi,\psi) & f_9(\theta,\phi,\psi)\cr}}\right]
\end{displaymath}](e_2004.gif) |
(33) |
as a 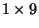 Vector
Vector
![\begin{displaymath}
{\bf f}=\left[{\matrix{f_1(\theta,\phi,\psi)\cr \vdots\cr f_9(\theta,\phi,\psi)\cr}}\right].
\end{displaymath}](e_2006.gif) |
(34) |
Now set up the matrices
![\begin{displaymath}
\left[{\matrix{
\left.{\partial f_1\over\partial\theta}\righ...
...\left[{\matrix{d\theta\cr d\phi\cr d\psi\cr}}\right]=d{\bf f}.
\end{displaymath}](e_2007.gif) |
(35) |
Using Nonlinear Least Squares Fitting then gives solutions which converge to
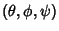 .
.
See also Cayley-Klein Parameters, Euler Parameters, Euler's Rotation Theorem,
Infinitesimal Rotation, Quaternion, Rotation, Rotation Matrix
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 198-200, 1985.
Goldstein, H. ``The Euler Angles'' and ``Euler Angles in Alternate Conventions.'' §4-4 and Appendix B in
Classical Mechanics, 2nd ed. Reading, MA: Addison-Wesley, pp. 143-148 and 606-610, 1980.
Landau, L. D. and Lifschitz, E. M. Mechanics, 3rd ed. Oxford, England: Pergamon Press, 1976.
© 1996-9 Eric W. Weisstein
1999-05-25
![\begin{displaymath}
{\hbox{\sf A}}\equiv \left[{\matrix{
a_{11} & a_{12} & a_{13...
...21} & a_{22} & a_{23}\cr
a_{31} & a_{32} & a_{33}\cr}}\right].
\end{displaymath}](e_1911.gif)
![]() -convention,'' illustrated above,
-convention,'' illustrated above,
![$\displaystyle \left[\begin{array}{ccc}\cos\phi & \sin\phi & 0\\ -\sin\phi & \cos\phi & 0\\ 0 & 0 & 1\end{array}\right]$](e_1913.gif)
![$\displaystyle \left[\begin{array}{ccc}1 & 0 & 0\\ 0 & \cos\theta & \sin\theta\\ 0 & -\sin\theta & \cos\theta\end{array}\right]$](e_1915.gif)
![$\displaystyle \left[\begin{array}{ccc}\cos\psi & \sin\psi & 0\\ -\sin\psi & \cos\psi & 0\\ 0 & 0 & 1\end{array}\right],$](e_1917.gif)
![$\displaystyle \left[\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_...
...right] \left[\begin{array}{c}\omega_x\\ \omega_y\\ \omega_z\end{array}\right]$](e_1937.gif)
![$\displaystyle \left[\begin{array}{c} a_{11}\omega_x+a_{12}\omega_y+a_{13}\omega...
...ga_z\\ a_{31}\omega_x+a_{32}\omega_y+a_{33}\omega_z\end{array}\right]\nonumber$](e_1938.gif)
![\begin{displaymath}
\boldsymbol{\omega}_\phi = {\bf A}_1\omega_z = \left[{\matri...
...theta\cr \cos\psi\sin\theta\cr\cos \theta\cr}}\right]\dot\phi.
\end{displaymath}](e_1942.gif)
![\begin{displaymath}
\boldsymbol{\omega}_\theta = {\bf B}_1\omega_\xi = {\bf B}_1...
...eft[{\matrix{\cos\psi\cr -\sin\psi\cr 0\cr}}\right]\dot\theta.
\end{displaymath}](e_1946.gif)
![\begin{displaymath}
\boldsymbol{\omega}_\psi={\bf B}_3\omega_\psi = {\bf B}_3\dot\psi = \left[{\matrix{0\cr 0\cr 1\cr}}\right]\dot\psi.
\end{displaymath}](e_1949.gif)
![\begin{displaymath}
\boldsymbol{\omega}=\left[{\matrix{\sin\psi\sin\theta \dot\p...
...dot\phi-\sin\psi\cr
\cos\theta \dot\phi+\dot\psi.\cr}}\right]
\end{displaymath}](e_1950.gif)
![]() -convention Euler angles are given in terms of the Cayley-Klein Parameters by
-convention Euler angles are given in terms of the Cayley-Klein Parameters by
![$\displaystyle -2i\ln\left[{\pm {\alpha^{1/2}\gamma^{1/4}\over\beta^{1/4}(1+\bet...
...t[{\pm {i\alpha^{1/2}\gamma^{1/4}\over\beta^{1/4}(1+\beta\gamma)^{1/4}}}\right]$](e_1951.gif)
![$\displaystyle -2i\ln\left[{\pm {\alpha^{1/2}\beta^{1/4}\over\gamma^{1/4}(1+\bet...
...t[{\pm {i\alpha^{1/2}\beta^{1/4}\over\gamma^{1/4}(1+\beta\gamma)^{1/4}}}\right]$](e_1953.gif)
![]() -convention,''
-convention,''
![$\displaystyle \left[\begin{array}{ccc}-\sin\phi & \cos\phi & 0\\ -\cos\phi & -\sin\phi & 0\\ 0 & 0 & 1\end{array}\right]$](e_1962.gif)
![$\displaystyle \left[\begin{array}{ccc}1 & 0 & 0\\ 0 & \cos\theta & \sin\theta\\ 0 & -\sin\theta & \cos\theta\end{array}\right]$](e_1915.gif)
![$\displaystyle \left[\begin{array}{ccc}\sin\psi & -\cos\psi & 0\\ \cos\psi & \sin\psi & 0\\ 0 & 0 & 1\end{array}\right]$](e_1963.gif)
![]() '' (pitch-roll-yaw) convention,
'' (pitch-roll-yaw) convention, ![]() is pitch,
is pitch, ![]()
![]() is
roll,
is
roll, ![]() and
and ![]() is yaw.
is yaw. ![]()
![$\displaystyle \left[\begin{array}{ccc}\cos\phi & \sin\phi & 0\\ -\sin\phi & \cos\phi & 0\\ 0 & 0 & 1\end{array}\right]$](e_1913.gif)
![$\displaystyle \left[\begin{array}{ccc}\cos\theta & 0 & -\sin\theta\\ 0 & 1 & 0\\
\sin\theta & 0 & \cos\theta\end{array}\right]$](e_1970.gif)
![$\displaystyle \left[\begin{array}{ccc}1 & 0 & 0\\ 0 & \cos\psi & \sin\psi\\ 0 & -\sin\psi & \cos\psi\end{array}\right]$](e_1971.gif)
![]() ,
, ![]() ,
, ![]() and
and ![]() ,
defined by
,
defined by
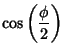
![$\displaystyle \left[\begin{array}{c}e_1\\ e_2\\ e_3\end{array}\right] = \hat {\bf n} \sin\left({\phi\over 2}\right).$](e_1988.gif)
![]() points
points ![]() and
and ![]() are known, one rotated with respect to the other,
then the Euler rotation matrix can be obtained in a straightforward manner using Least Squares Fitting. Write the
points as arrays of vectors, so
are known, one rotated with respect to the other,
then the Euler rotation matrix can be obtained in a straightforward manner using Least Squares Fitting. Write the
points as arrays of vectors, so
![\begin{displaymath}
{\hbox{\sf A}}=\left[{\matrix{
f_1(\theta,\phi,\psi) & f_2(\...
...i) & f_7(\theta,\phi,\psi) & f_9(\theta,\phi,\psi)\cr}}\right]
\end{displaymath}](e_2004.gif)
![\begin{displaymath}
{\bf f}=\left[{\matrix{f_1(\theta,\phi,\psi)\cr \vdots\cr f_9(\theta,\phi,\psi)\cr}}\right].
\end{displaymath}](e_2006.gif)
![\begin{displaymath}
\left[{\matrix{
\left.{\partial f_1\over\partial\theta}\righ...
...\left[{\matrix{d\theta\cr d\phi\cr d\psi\cr}}\right]=d{\bf f}.
\end{displaymath}](e_2007.gif)
![]() .
.