In Spherical Coordinates, the Scale Factors are 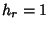 ,
,
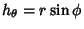 ,
,  , and
the separation functions are
, and
the separation functions are 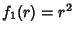 ,
, 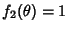 ,
,
 , giving a Stäckel
Determinant of
, giving a Stäckel
Determinant of 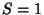 . The Laplacian is
. The Laplacian is
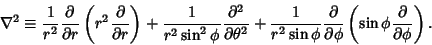 |
(1) |
To solve the Helmholtz Differential Equation in Spherical
Coordinates, attempt Separation of Variables by writing
 |
(2) |
Then the Helmholtz Differential Equation becomes
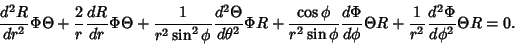 |
(3) |
Now divide by 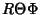 ,
,
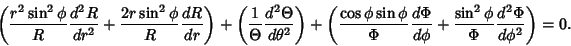 |
(5) |
The solution to the second part of (5) must be sinusoidal, so the differential equation is
 |
(6) |
which has solutions which may be defined either as a Complex function with 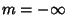 , ...,
, ..., 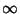
 |
(7) |
or as a sum of Real sine and cosine functions with 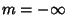 , ...,
, ..., 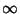
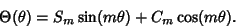 |
(8) |
Plugging (6) back into (7),
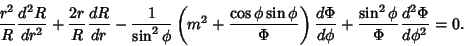 |
(9) |
The radial part must be equal to a constant
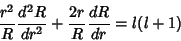 |
(10) |
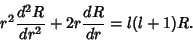 |
(11) |
But this is the Euler Differential Equation, so we try a series solution of the form
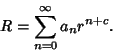 |
(12) |
Then
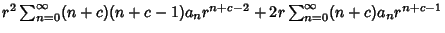
|
|
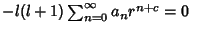
|
(13) |
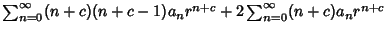
|
|
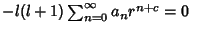
|
(14) |
![\begin{displaymath}
\sum_{n=0}^\infty [(n+c)(n+c+1)-l(l+1)]a_nr^{n+c}= 0.
\end{displaymath}](h_1129.gif) |
(15) |
This must hold true for all Powers of 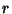 . For the
. For the 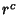 term (with
term (with 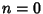 ),
),
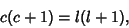 |
(16) |
which is true only if  and all other terms vanish. So
and all other terms vanish. So 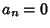 for
for  ,
, 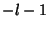 . Therefore, the
solution of the
. Therefore, the
solution of the 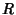 component is given by
component is given by
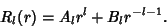 |
(17) |
Plugging (17) back into (9),
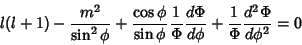 |
(18) |
![\begin{displaymath}
\Phi''+{\cos\phi\over\sin\phi}\Phi'+\left[{l(l+1)-{m^2\over\sin^2\phi}}\right]\Phi = 0,
\end{displaymath}](h_1137.gif) |
(19) |
which is the associated Legendre Differential Equation for 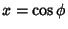 and
and 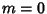 , ...,
, ..., 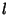 . The general
Complex solution is therefore
. The general
Complex solution is therefore
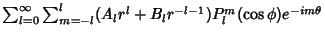
|
|
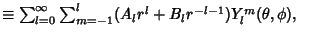
|
(20) |
where
 |
(21) |
are the (Complex) Spherical Harmonics. The general Real solution is
![\begin{displaymath}
\sum_{l=0}^\infty \sum_{m=0}^l (A_lr^l+B_lr^{-l-1})P_l^m(\cos \phi)[S_m\sin(m\theta)+C_m\cos(m\theta)].
\end{displaymath}](h_1143.gif) |
(22) |
Some of the normalization constants of 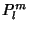 can be absorbed by
can be absorbed by 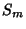 and
and 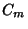 , so this equation may appear in the
form
, so this equation may appear in the
form
![$\sum_{l=0}^\infty \sum_{m=0}^l (A_lr^l+B_lr^{-l-1})P_l^m (\cos \phi)[S_l^m\sin(m\theta)+C_l^m\cos(m\theta)]$](h_1147.gif)
|
|
![$ \equiv \sum_{l=0}^\infty \sum_{m=0}^l (A_lr^l+B_lr^{-l-1})\times[S_l^mY_l^{m(o)}(\theta, \phi )+C_l^mY_l^{m(e)}(\theta, \phi)],\quad$](h_1148.gif)
|
(23) |
where
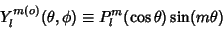 |
(24) |
 |
(25) |
are the Even and Odd (real) Spherical Harmonics. If azimuthal symmetry is present, then
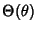 is constant and the solution of the
is constant and the solution of the 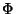 component is a Legendre Polynomial
component is a Legendre Polynomial
 . The
general solution is then
. The
general solution is then
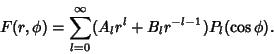 |
(26) |
Actually, the equation is separable under the more general condition that 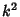 is of the form
is of the form
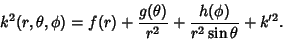 |
(27) |
References
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 514 and 658, 1953.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() ,
,
![]() ,
, ![]() , and
the separation functions are
, and
the separation functions are ![]() ,
, ![]() ,
,
![]() , giving a Stäckel
Determinant of
, giving a Stäckel
Determinant of ![]() . The Laplacian is
. The Laplacian is
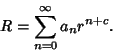
![\begin{displaymath}
\sum_{n=0}^\infty [(n+c)(n+c+1)-l(l+1)]a_nr^{n+c}= 0.
\end{displaymath}](h_1129.gif)
![\begin{displaymath}
\sum_{l=0}^\infty \sum_{m=0}^l (A_lr^l+B_lr^{-l-1})P_l^m(\cos \phi)[S_m\sin(m\theta)+C_m\cos(m\theta)].
\end{displaymath}](h_1143.gif)
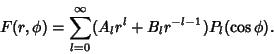
![]() is of the form
is of the form