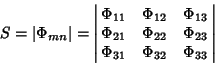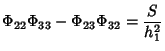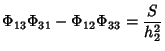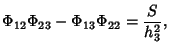A Determinant used to determine in which coordinate systems the Helmholtz Differential Equation is separable
(Morse and Feshbach 1953). A determinant
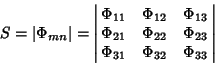 |
(1) |
in which 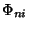 are functions of
are functions of 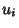 alone is called a Stäckel determinant. A coordinate system is separable if it
obeys the Robertson Condition, namely that the Scale Factors
alone is called a Stäckel determinant. A coordinate system is separable if it
obeys the Robertson Condition, namely that the Scale Factors 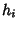 in the Laplacian
in the Laplacian
 |
(2) |
can be rewritten in terms of functions 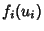 defined by
defined by
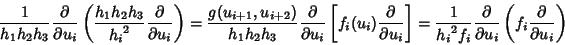 |
(3) |
such that  can be written
can be written
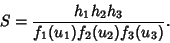 |
(4) |
When this is true, the separated equations are of the form
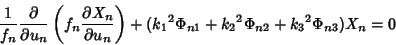 |
(5) |
The 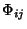 s obey the minor equations
s obey the minor equations
which are equivalent to
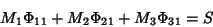 |
(9) |
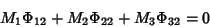 |
(10) |
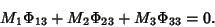 |
(11) |
This gives a total of four equations in nine unknowns. Morse and Feshbach (1953, pp. 655-666) give not only the Stäckel
determinants for common coordinate systems, but also the elements of the determinant (although it is not clear how these are
derived).
See also Helmholtz Differential Equation, Laplace's Equation, Poisson's Equation,
Robertson Condition, Separation of Variables
References
Morse, P. M. and Feshbach, H. ``Tables of Separable Coordinates in Three Dimensions.''
Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 509-511 and 655-666, 1953.
© 1996-9 Eric W. Weisstein
1999-05-26