The general nonhomogeneous equation is
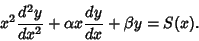 |
(1) |
The homogeneous equation is
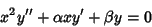 |
(2) |
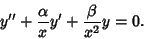 |
(3) |
Now attempt to convert the equation from
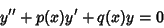 |
(4) |
to one with constant Coefficients
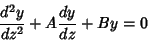 |
(5) |
by using the standard transformation for linear Second-Order Ordinary Differential Equations. Comparing (3) and (5), the functions  and
and 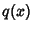 are
are
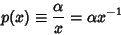 |
(6) |
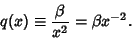 |
(7) |
Let 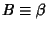 and define
and define
Then 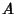 is given by
is given by
which is a constant. Therefore, the equation becomes a second-order ODE with constant Coefficients
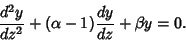 |
(10) |
Define
and
The solutions are
In terms of the original variable  ,
,
© 1996-9 Eric W. Weisstein
1999-05-25

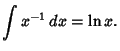
![$\displaystyle {q'(x)+2p(x)q(x)\over 2[q(x)]^{3/2}} B^{1/2}$](e_2067.gif)
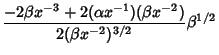
![$\displaystyle \left\{\begin{array}{ll} c_1e^{r_1z}+c_2e^{r_2z} & \mbox{$(\alpha...
...{az}[c_1\cos(bz)+c_2\sin(bz)] & \mbox{$(\alpha-1)^2<4\beta$.}\end{array}\right.$](e_2078.gif)
![$\displaystyle \left\{\begin{array}{ll} c_1\vert x\vert^{r_1}+c_2\vert x\vert^{r...
...t)+c_2\sin(b\ln\vert x\vert)] & \mbox{$(\alpha-1)^2<4\beta$.}\end{array}\right.$](e_2079.gif)