An ODE
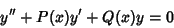 |
(1) |
has singularities for finite 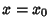 under the following conditions: (a) If either
under the following conditions: (a) If either 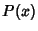 or
or 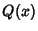 diverges as
diverges as  , but
, but 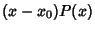 and
and 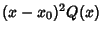 remain finite as
remain finite as  , then
, then 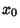 is called a regular or nonessential
singular point. (b) If
is called a regular or nonessential
singular point. (b) If 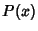 diverges faster than
diverges faster than 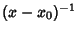 so that
so that
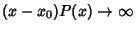 as
as  , or
, or
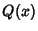 diverges faster than
diverges faster than 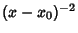 so that
so that
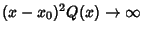 as
as  , then
, then 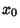 is called an
irregular or essential singularity.
is called an
irregular or essential singularity.
Singularities of equation (1) at infinity are investigated by making the substitution
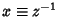 , so
, so
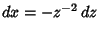 , giving
, giving
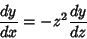 |
(2) |
Then (1) becomes
![\begin{displaymath}
z^4 {d^2y\over dz^2} + [2z^3-z^2P(z)]{dy\over dz} + Q(z)y = 0.
\end{displaymath}](o_728.gif) |
(4) |
Case (a): If
remain finite at
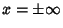 (
(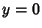 ), then the point is ordinary. Case (b): If either
), then the point is ordinary. Case (b): If either 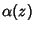 diverges no more
rapidly than
diverges no more
rapidly than 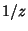 or
or 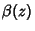 diverges no more rapidly than
diverges no more rapidly than 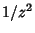 , then the point is a regular singular point.
Case (c): Otherwise, the point is an irregular singular point.
, then the point is a regular singular point.
Case (c): Otherwise, the point is an irregular singular point.
Morse and Feshbach (1953, pp. 667-674) give the canonical forms and solutions for second-order ODEs classified by
types of singular points.
For special classes of second-order linear ordinary differential equations, variable Coefficients can
be transformed into constant Coefficients. Given a second-order linear ODE with variable
Coefficients
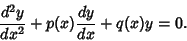 |
(7) |
Define a function 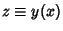 ,
,
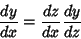 |
(8) |
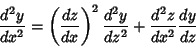 |
(9) |
![\begin{displaymath}
\left({dz\over dx}\right)^2 {d^2y\over dz^2} + \left[{{d^2z\over dx^2} + p(x){dz\over dx}}\right]{dy\over dz} + q(x)y = 0
\end{displaymath}](o_743.gif) |
(10) |
![\begin{displaymath}
{d^2y\over dz^2} + \left[{{d^2z\over dx^2} + p(x){dz\over dx...
...^2}\right]y \equiv {d^2y\over dz^2} + A {dy\over dz} + By = 0.
\end{displaymath}](o_744.gif) |
(11) |
This will have constant Coefficients if 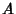 and
and 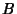 are not functions of
are not functions of 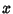 . But we are free to set
. But we are free to set
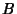 to an arbitrary Positive constant for
to an arbitrary Positive constant for 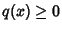 by defining
by defining 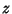 as
as
![\begin{displaymath}
z \equiv B^{-1/2}\int [q(x)]^{1/2}\,dx.
\end{displaymath}](o_746.gif) |
(12) |
Then
![\begin{displaymath}
{dz\over dx} = B^{-1/2}[q(x)]^{1/2}
\end{displaymath}](o_747.gif) |
(13) |
![\begin{displaymath}
{d^2z\over dx^2} = {\textstyle{1\over 2}}B^{-1/2}[q(x)]^{-1/2}q'(x),
\end{displaymath}](o_748.gif) |
(14) |
and
Equation (11) therefore becomes
![\begin{displaymath}
{d^2y\over dz^2} + {q'(x)+2p(x)q(x)\over 2[q(x)]^{3/2}} B^{1/2} {dy\over dz} + By = 0,
\end{displaymath}](o_751.gif) |
(16) |
which has constant Coefficients provided that
![\begin{displaymath}
A \equiv {q'(x)+2p(x)q(x)\over 2[q(x)]^{3/2}} B^{1/2} = {\rm [constant]}.
\end{displaymath}](o_752.gif) |
(17) |
Eliminating constants, this gives
![\begin{displaymath}
A'\equiv {q'(x)+2p(x)q(x)\over [q(x)]^{3/2}} = {\rm [constant]}.
\end{displaymath}](o_753.gif) |
(18) |
So for an ordinary differential equation in which 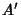 is a constant, the solution is given by solving the second-order
linear ODE with constant Coefficients
is a constant, the solution is given by solving the second-order
linear ODE with constant Coefficients
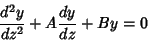 |
(19) |
for 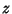 , where
, where 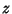 is defined as above.
is defined as above.
A linear second-order homogeneous differential equation of the general form
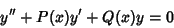 |
(20) |
can be transformed into standard form
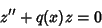 |
(21) |
with the first-order term eliminated using the substitution
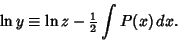 |
(22) |
Then
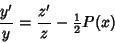 |
(23) |
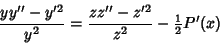 |
(24) |
 |
(25) |
so
Therefore,
![\begin{displaymath}
z''+[Q(x)-{\textstyle{1\over 2}}P'(x)-{\textstyle{1\over 4}}P^2(x)]z \equiv z''(x)+q(x)z = 0,
\end{displaymath}](o_765.gif) |
(28) |
where
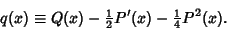 |
(29) |
If 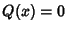 , then the differential equation becomes
, then the differential equation becomes
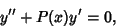 |
(30) |
which can be solved by multiplying by
![\begin{displaymath}
\mathop{\rm exp}\nolimits \left[{\int^x P(x')\,dx'}\right]
\end{displaymath}](o_768.gif) |
(31) |
to obtain
![\begin{displaymath}
0 = {d\over dx}\left\{{\mathop{\rm exp}\nolimits \left[{\int^x P(x')\,dx'}\right]{dy\over dx}}\right\}
\end{displaymath}](o_769.gif) |
(32) |
![\begin{displaymath}
c_1 = \mathop{\rm exp}\nolimits \left[{\int^x P(x')\,dx'}\right]{dy\over dx}
\end{displaymath}](o_770.gif) |
(33) |
![\begin{displaymath}
y = c_1\int^x {dx\over \mathop{\rm exp}\nolimits \left[{\int^x P(x')\,dx'}\right]}+c_2.
\end{displaymath}](o_771.gif) |
(34) |
If one solution (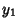 ) to a second-order ODE is known, the other (
) to a second-order ODE is known, the other ( ) may be found using the Reduction of
Order method. From the Abel's Identity
) may be found using the Reduction of
Order method. From the Abel's Identity
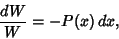 |
(35) |
where
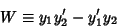 |
(36) |
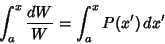 |
(37) |
![\begin{displaymath}
\ln\left[{W(x)\over W(a)}\right]= \int^x_a P(x')\,dx'
\end{displaymath}](o_777.gif) |
(38) |
![\begin{displaymath}
W(x) = W(a)\mathop{\rm exp}\nolimits \left[{- \int^x_a P(x')\,dx'}\right].
\end{displaymath}](o_778.gif) |
(39) |
But
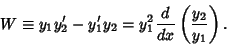 |
(40) |
Combining (39) and (40) yields
![\begin{displaymath}
{d\over dx}\left({y_2\over y1}\right)= W(a) {\mathop{\rm exp}\nolimits [- \int^x_a P(x')\,dx']\over y_1^2}
\end{displaymath}](o_780.gif) |
(41) |
![\begin{displaymath}
y_2(x) = y_1(x)W(a)\int_b^x {\mathop{\rm exp}\nolimits [- \int^{x'}_a P(x'')\,dx'']\over [y_1(x')]^2}\,dx'.
\end{displaymath}](o_781.gif) |
(42) |
Disregarding 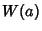 , since it is simply a multiplicative constant, and the constants
, since it is simply a multiplicative constant, and the constants  and
and 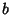 , which will contribute a
solution which is not linearly independent of
, which will contribute a
solution which is not linearly independent of 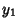 ,
,
![\begin{displaymath}
y_2(x) = y_1(x)\int^x {\mathop{\rm exp}\nolimits \left[{- \int^{x'} P(x'')\,dx''}\right]\over [y_1(x')]^2}\,dx'.
\end{displaymath}](o_783.gif) |
(43) |
If 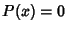 , this simplifies to
, this simplifies to
![\begin{displaymath}
y_2(x) = y_1(x) \int^x{dx'\over [y_1(x')]^2}.
\end{displaymath}](o_785.gif) |
(44) |
For a nonhomogeneous second-order ODE in which the 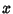 term does not appear in the function
term does not appear in the function 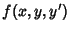 ,
,
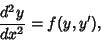 |
(45) |
let 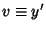 , then
, then
 |
(46) |
So the first-order ODE
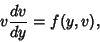 |
(47) |
if linear, can be solved for 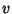 as a linear first-order ODE. Once the solution is known,
as a linear first-order ODE. Once the solution is known,
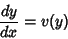 |
(48) |
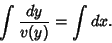 |
(49) |
On the other hand, if 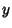 is missing from
is missing from 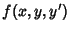 ,
,
 |
(50) |
let 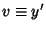 , then
, then  , and the equation reduces to
, and the equation reduces to
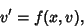 |
(51) |
which, if linear, can be solved for 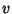 as a linear first-order ODE. Once the solution is known,
as a linear first-order ODE. Once the solution is known,
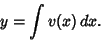 |
(52) |
See also Abel's Identity, Adjoint Operator
References
Arfken, G. ``A Second Solution.'' §8.6 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 467-480, 1985.
Boyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 4th ed.
New York: Wiley, 1986.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 667-674, 1953.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() , so
, so
![]() , giving
, giving
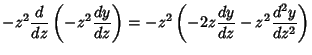
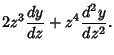
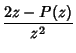
![\begin{displaymath}
{d^2y\over dz^2} + \left[{{d^2z\over dx^2} + p(x){dz\over dx...
...^2}\right]y \equiv {d^2y\over dz^2} + A {dy\over dz} + By = 0.
\end{displaymath}](o_744.gif)
![$\displaystyle {{\textstyle{1\over 2}}B^{-1/2}[q(x)]^{-1/2}q'(x)+B^{-1/2}p(x)[q(x)]^{1/2}\over B^{-1}q(x)}$](o_749.gif)
![$\displaystyle {q'(x)+2p(x)q(x)\over 2[q(x)]^{3/2}} B^{1/2}.$](o_750.gif)
![$\displaystyle {y''\over y}=\left[{{z'\over z}-{\textstyle{1\over 2}}P(x)}\right]^2+{z''\over z}-{z'^2\over z^2}-{\textstyle{1\over 2}}P'(x)$](o_761.gif)
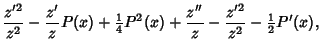
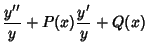
![$\displaystyle -{z'\over z}P(x)+{\textstyle{1\over 4}}P^2(x)+{z''\over z}-{\text...
...{1\over 2}}P'(x)+P(x)\left[{{z'\over z}-{\textstyle{1\over 2}}P(x)}\right]+Q(x)$](o_764.gif)
![]() , then the differential equation becomes
, then the differential equation becomes
![]() ) to a second-order ODE is known, the other (
) to a second-order ODE is known, the other (![]() ) may be found using the Reduction of
Order method. From the Abel's Identity
) may be found using the Reduction of
Order method. From the Abel's Identity
![\begin{displaymath}
y_2(x) = y_1(x)W(a)\int_b^x {\mathop{\rm exp}\nolimits [- \int^{x'}_a P(x'')\,dx'']\over [y_1(x')]^2}\,dx'.
\end{displaymath}](o_781.gif)
![\begin{displaymath}
y_2(x) = y_1(x)\int^x {\mathop{\rm exp}\nolimits \left[{- \int^{x'} P(x'')\,dx''}\right]\over [y_1(x')]^2}\,dx'.
\end{displaymath}](o_783.gif)
![]() term does not appear in the function
term does not appear in the function ![]() ,
,
![]() is missing from
is missing from ![]() ,
,