|
|
|
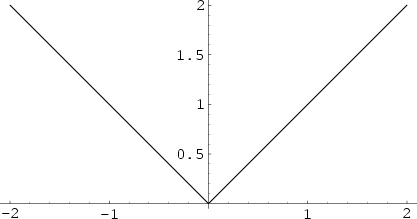
The absolute value of a Real Number ![]() is denoted
is denoted ![]() and given by
and given by
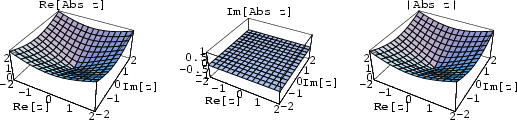
The same notation is used to denote the Modulus of a Complex Number ![]() ,
,
![]() , a p-adic Number absolute value, or a general Valuation. The
Norm of a Vector
, a p-adic Number absolute value, or a general Valuation. The
Norm of a Vector ![]() is also denoted
is also denoted ![]() , although
, although ![]() is more commonly used.
is more commonly used.
Other Notations similar to the absolute value are the Floor Function
![]() ,
Nint function
,
Nint function ![]() , and Ceiling Function
, and Ceiling Function
![]() .
.
See also Absolute Square, Ceiling Function, Floor Function, Modulus (Complex Number), Nint, Sgn, Triangle Function, Valuation