|
|
|
The Euler-Mascheroni constant is denoted ![]() (or sometimes
(or sometimes ![]() ) and has the numerical value
) and has the numerical value
| (1) |
It is not known if this constant is Irrational, let alone Transcendental. However, Conway and Guy (1996) are ``prepared to bet that it is transcendental,'' although they do not expect a proof to be achieved within their lifetimes.
The Euler-Mascheroni constant arises in many integrals
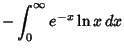 |
(2) | ||
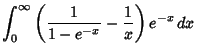 |
(3) | ||
 |
(4) |
![$\displaystyle 1 + \sum_{k=2}^\infty \left[{{1\over k} + \ln\left({k-1\over k}\right)}\right]$](e_2236.gif) |
(5) | ||
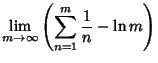 |
(6) | ||
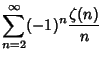 |
(7) | ||
 |
(8) | ||
![$\displaystyle \lim_{n\to\infty}\left[{\,\sum_{k=1}^n k^{-1} - \ln n - {1\over 2n} + \sum_{k=1}^n {B_{2k}\over (2k)n^{2k}}}\right],$](e_2240.gif) |
|||
| (9) |
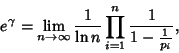 |
(10) |
| (11) |
Infinite Products involving ![]() also arise from the G-Function
with Positive Integer
also arise from the G-Function
with Positive Integer ![]() . The cases
. The cases ![]() and
and ![]() give
give
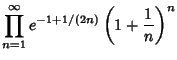 |
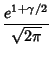 |
(12) | |
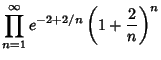 |
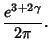 |
(13) |
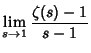 |
(14) | ||
| (15) | |||
![$\displaystyle \lim_{x\to\infty}\left[{x-\Gamma\left({1\over x}\right)}\right]$](e_2253.gif) |
(16) |
The difference between the ![]() th convergent in (6) and
th convergent in (6) and ![]() is given by
is given by
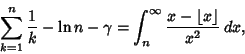 |
(17) |
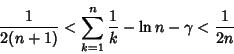 |
(18) |
![\begin{displaymath}
\gamma={\textstyle{3\over 2}}-\ln 2-\sum_{m=2}^\infty (-1)^m{m-1\over m}[\zeta(m)-1]
\end{displaymath}](e_2256.gif) |
(19) |
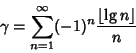 |
(20) |
 |
(21) |
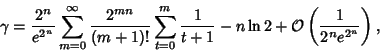 |
(22) |
The symbol ![]() is sometimes also used for
is sometimes also used for
| (23) |
Odena (1982-1983) gave the strange approximation
| (24) |
| (25) | |||
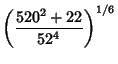 |
(26) | ||
 |
(27) | ||
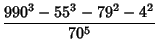 |
|||
| (28) |
No quadratically converging algorithm for computing ![]() is known (Bailey 1988). 7,000,000 digits of
is known (Bailey 1988). 7,000,000 digits of
![]() have been computed as of Feb. 1998 (Plouffe).
have been computed as of Feb. 1998 (Plouffe).
See also Euler Product, Mertens Theorem, Stieltjes Constants
References
Bailey, D. H. ``Numerical Results on the Transcendence of Constants Involving
Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, Feb. 1972.
Brent, R. P. ``Computation of the Regular Continued Fraction for Euler's Constant.'' Math. Comput. 31, 771-777, 1977.
Brent, R. P. and McMillan, E. M. ``Some New Algorithms for High-Precision Computation of Euler's Constant.''
Math. Comput. 34, 305-312, 1980.
Castellanos, D. ``The Ubiquitous Pi. Part I.'' Math. Mag. 61, 67-98, 1988.
Conway, J. H. and Guy, R. K. ``The Euler-Mascheroni Number.'' In The Book of Numbers. New York: Springer-Verlag,
pp. 260-261, 1996.
de la Vallée Poussin, C.-J. Untitled communication. Annales de la Soc. Sci. Bruxelles 22, 84-90, 1898.
DeTemple, D. W. ``A Quicker Convergence to Euler's Constant.'' Amer. Math. Monthly 100, 468-470, 1993.
Dirichlet, G. L. J. für Math. 18, 273, 1838.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/euler/euler.html
Flajolet, P. and Vardi, I. ``Zeta Function Expansions of Classical Constants.'' Unpublished manuscript, 1996.
http://pauillac.inria.fr/algo/flajolet/Publications/landau.ps.
Gerst, I. ``Some Series for Euler's Constant.'' Amer. Math. Monthly 76, 273-275, 1969.
Glaisher, J. W. L. ``On the History of Euler's Constant.'' Messenger of Math. 1, 25-30, 1872.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, 1979.
Knuth, D. E. ``Euler's Constant to 1271 Places.'' Math. Comput. 16, 275-281, 1962.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 28, 1983.
Plouffe, S. ``Plouffe's Inverter: Table of Current Records for the Computation
of Constants.'' http://www.lacim.uqam.ca/pi/records.html.
Sloane, N. J. A. Sequences
A033091,
A033092,
A033149,
A046114,
A046114,
A001620/M3755, and
A002852/M0097
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
Sweeney, D. W. ``On the Computation of Euler's Constant.'' Math. Comput. 17, 170-178, 1963.
Vacca, G. ``A New Series for the Eulerian Constant.'' Quart. J. Pure Appl. Math. 41, 363-368, 1910.
Young, R. M. ``Euler's Constant.'' Math. Gaz. 75, 187-190, 1991.
![]() ,
, ![]() , and Euler's Constant.''
Math. Comput. 50, 275-281, 1988.
, and Euler's Constant.''
Math. Comput. 50, 275-281, 1988.
|
|
|
© 1996-9 Eric W. Weisstein