|
|
|
The term ``product'' refers to the result of one or more
Multiplications. For example, the mathematical statement
![]() would be read ``
would be read ``![]() Times
Times ![]() Equals
Equals ![]() ,'' where
,'' where ![]() is the
product.
is the
product.
The product symbol is defined by
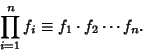
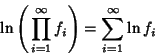
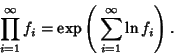
For ![]() , then the products
, then the products
![]() and
and
![]() converge and diverge
as
converge and diverge
as
![]() .
.
See also Cross Product, Dot Product, Inner Product, Matrix Product, Multiplication, Nonassociative Product, Outer Product, Sum, Tensor Product, Times, Vector Triple Product
References
Guy, R. K. ``Products Taken over Primes.'' §B87 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 102-103, 1994.