|
|
|
The factorial ![]() is defined for a Positive Integer
is defined for a Positive Integer ![]() as
as
| (1) |
As ![]() grows large, factorials begin acquiring tails of trailing Zeros. To calculate the number of
trailing Zeros for
grows large, factorials begin acquiring tails of trailing Zeros. To calculate the number of
trailing Zeros for ![]() , use
, use
 |
(2) |
| (3) |
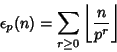 |
(4) |
| (5) |
By noting that
| (6) |
| (7) |
| (8) | |||
| (9) | |||
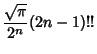 |
(10) | ||
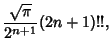 |
(11) |
For Integers ![]() and
and ![]() with
with ![]() ,
,
| (12) |
![$\displaystyle {1\over 2}\ln\left[{\pi z\over\sin(\pi z)}\right]-\gamma-\sum_{n=1}^\infty {\zeta(2n+1)\over 2n+1} z^{2n+1}$](f_72.gif) |
(13) | ||
![$\displaystyle {1\over 2}\ln\left[{\pi z\over\sin(\pi z)}\right]-{1\over 2}\ln\l...
... 1-z}\right)+(1-\gamma)z-\sum_{n=1}^\infty [\zeta(2n+1)-1] {z^{2n+1}\over 2n+1}$](f_73.gif) |
(14) | ||
![$\displaystyle \ln\left[{\lim_{n\to\infty} {n!\over (z+1)(z+2)\cdots (z+n)} n^z}\right]$](f_74.gif) |
(15) | ||
| (16) | |||
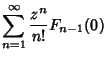 |
(17) | ||
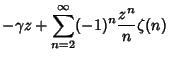 |
(18) | ||
![$\displaystyle -\ln(1+z)+z(1-\gamma) + \sum_{n=2}^\infty (-1)^n[\zeta(n)-1] {z^n\over n},$](f_78.gif) |
(19) |
| (20) |
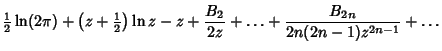 |
|||
| (21) |
Identities satisfied by sums of factorials include
| (22) | |||
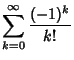 |
(23) | ||
 |
(24) | ||
 |
(25) | ||
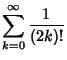 |
(26) | ||
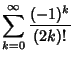 |
(27) | ||
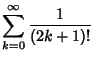 |
(28) | ||
 |
(29) |
Let ![]() be the exponent of the greatest Power of a Prime
be the exponent of the greatest Power of a Prime ![]() dividing
dividing ![]() . Then
. Then
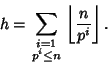 |
(30) |
| (31) |
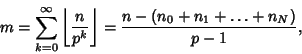 |
(32) |
The sum-of-factorials function is defined by
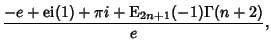 |
(33) | ||
![$\displaystyle {-e+\mathop{\rm ei}\nolimits (1)+\Re[{\rm E}_{2n+1}(-1)]\Gamma(n+2)\over e},$](f_116.gif) |
(34) |
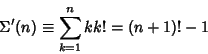 |
(35) |
The numbers ![]() are prime for
are prime for ![]() , 2, 3, 11, 27, 37, 41, 73, 77, 116, 154, ... (Sloane's A002981), and the numbers
, 2, 3, 11, 27, 37, 41, 73, 77, 116, 154, ... (Sloane's A002981), and the numbers ![]() are prime for
are prime for ![]() , 4, 6, 7, 12, 14, 30, 32, 33, 38, 94, 166, ... (Sloane's A002982). In general, the power-product sequences
(Mudge 1997) are given by
, 4, 6, 7, 12, 14, 30, 32, 33, 38, 94, 166, ... (Sloane's A002982). In general, the power-product sequences
(Mudge 1997) are given by
![]() . The first few terms of
. The first few terms of ![]() are 2, 5, 37, 577, 14401, 518401,
... (Sloane's A020549), and
are 2, 5, 37, 577, 14401, 518401,
... (Sloane's A020549), and ![]() is Prime for
is Prime for ![]() , 2, 3, 4, 5, 9, 10, 11, 13, 24, 65, 76, ... (Sloane's A046029).
The first few terms of
, 2, 3, 4, 5, 9, 10, 11, 13, 24, 65, 76, ... (Sloane's A046029).
The first few terms of ![]() are 0, 3, 35, 575, 14399, 518399, ... (Sloane's A046032), but
are 0, 3, 35, 575, 14399, 518399, ... (Sloane's A046032), but ![]() is Prime for
only
is Prime for
only ![]() since
since
![]() for
for ![]() . The first few terms of
. The first few terms of ![]() are 0, 7, 215, 13823, 1727999,
... (Sloane's A0460333), and the first few terms of
are 0, 7, 215, 13823, 1727999,
... (Sloane's A0460333), and the first few terms of ![]() are 2, 9, 217, 13825, 1728001, ... (Sloane's A019514).
are 2, 9, 217, 13825, 1728001, ... (Sloane's A019514).
There are only four Integers equal to the sum of the factorials of their digits. Such numbers are called
Factorions. While no factorial is a Square Number, D. Hoey listed sums ![]() of distinct
factorials which give Square Numbers, and J. McCranie gave the one additional sum less than
of distinct
factorials which give Square Numbers, and J. McCranie gave the one additional sum less than
![]() :
:
 |
(36) |
There are no identities of the form
| (37) |
| (38) | |||
| (39) | |||
| (40) |
There are three numbers less than 200,000 for which
| (41) |
| (42) |
See also Alladi-Grinstead Constant, Brocard's Problem, Brown Numbers, Double Factorial, Factorial Prime, Factorion, Gamma Function, Hyperfactorial, Multifactorial, Pochhammer Symbol, Primorial, Roman Factorial, Stirling's Series, Subfactorial, Superfactorial
References
Conway, J. H. and Guy, R. K. ``Factorial Numbers.'' In The Book of Numbers. New York:
Springer-Verlag, pp. 65-66, 1996.
Dudeney, H. E. Amusements in Mathematics. New York: Dover, p. 96, 1970.
Gardner, M. ``Factorial Oddities.'' Ch. 4 in
Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American.
New York: Vintage, pp. 50-65, 1978.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. ``Factorial Factors.'' §4.4 in
Concrete Mathematics: A Foundation for Computer Science. Reading, MA: Addison-Wesley, pp. 111--115, 1990.
Guy, R. K. ``Equal Products of Factorials,'' ``Alternating Sums of Factorials,'' and ``Equations Involving Factorial
Honsberger, R. Mathematical Gems II. Washington, DC: Math. Assoc. Amer., p. 2, 1976.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 56, 1983.
Leyland, P.
ftp://sable.ox.ac.uk/pub/math/factors/factorial-.Z and
ftp://sable.ox.ac.uk/pub/math/factors/factorial+.Z.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 174, 1979.
Mudge, M. ``Not Numerology but Numeralogy!'' Personal Computer World, 279-280, 1997.
Ogilvy, C. S. and Anderson, J. T. Excursions in Number Theory. New York: Dover, 1988.
Petkovsek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A. K. Peters, p. 86, 1996.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Gamma Function, Beta Function, Factorials,
Binomial Coefficients.'' §6.1 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge
University Press, pp. 206-209, 1992.
Ribenboim, P. The Book of Prime Number Records, 2nd ed. New York: Springer-Verlag, pp. 22-24, 1989.
Sloane, N. J. A. Sequences
A014615,
A014597,
A033312,
A020549,
A000142/M1675, and
A007489/M2818
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
Spanier, J. and Oldham, K. B. ``The Factorial Function
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 67, 1991.
![]() .'' §B23, B43, and D25 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 80, 100,
and 193-194, 1994.
.'' §B23, B43, and D25 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 80, 100,
and 193-194, 1994.
![]() and Its Reciprocal.''
Ch. 2 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 19-33, 1987.
and Its Reciprocal.''
Ch. 2 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 19-33, 1987.
|
|
|
© 1996-9 Eric W. Weisstein