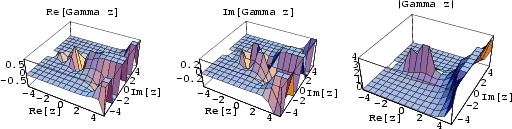
The complete gamma function is defined to be an extension of the Factorial to Complex and
Real Number arguments. It is Analytic everywhere except at  ,
, 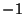 ,
, 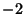 , ....
It can be defined as a Definite Integral for
, ....
It can be defined as a Definite Integral for ![$\Re[z] > 0$](g_195.gif) (Euler's integral form)
(Euler's integral form)
or
![\begin{displaymath}
\Gamma(z)\equiv \int^1_0 \left[{\ln\left({1\over t}\right)}\right]^{z-1}\,dt.
\end{displaymath}](g_199.gif) |
(3) |
Integrating (1) by parts for a Real argument, it can be seen that
If  is an Integer
is an Integer 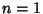 , 2, 3, ...then
, 2, 3, ...then
so the gamma function reduces to the Factorial for a Positive Integer argument.
Binet's Formula is
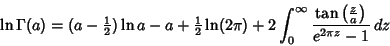 |
(6) |
for ![$\Re[a]>0$](g_208.gif) (Whittaker and Watson 1990, p. 251). The gamma function can
also be defined by an Infinite Product form (Weierstraß Form)
(Whittaker and Watson 1990, p. 251). The gamma function can
also be defined by an Infinite Product form (Weierstraß Form)
![\begin{displaymath}
\Gamma(z) \equiv \left[{ze^{\gamma z}\prod_{r=1}^\infty \left({1 + {z\over r}}\right)e^{-z/r}}\right]^{-1},
\end{displaymath}](g_209.gif) |
(7) |
where 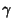 is the Euler-Mascheroni Constant. This can be written
is the Euler-Mascheroni Constant. This can be written
![\begin{displaymath}
\Gamma(z)={1\over z}\mathop{\rm exp}\nolimits \left[{\sum_{k=1}^\infty {(-1)^k s_k\over k} x^k}\right],
\end{displaymath}](g_210.gif) |
(8) |
where
for 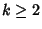 , where
, where 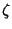 is the Riemann Zeta Function (Finch). Taking the logarithm of both sides of
(7),
is the Riemann Zeta Function (Finch). Taking the logarithm of both sides of
(7),
![\begin{displaymath}
-\ln[\Gamma(z)]=\ln z+\gamma z+\sum_{n=1}^\infty \left[{\ln\left({1+{z\over n}}\right)-{z\over n}}\right].
\end{displaymath}](g_217.gif) |
(11) |
Differentiating,
where 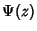 is the Digamma Function and
is the Digamma Function and 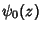 is the Polygamma Function.
is the Polygamma Function.  th derivatives are
given in terms of the Polygamma Functions
th derivatives are
given in terms of the Polygamma Functions 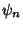 ,
, 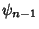 , ...,
, ..., 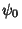 .
.
The minimum value 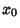 of
of 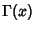 for Real Positive
for Real Positive  is achieved when
is achieved when
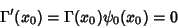 |
(17) |
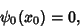 |
(18) |
This can be solved numerically to give
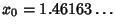 (Sloane's A030169), which has Continued Fraction [1, 2, 6,
63, 135, 1, 1, 1, 1, 4, 1, 38, ...] (Sloane's A030170). At
(Sloane's A030169), which has Continued Fraction [1, 2, 6,
63, 135, 1, 1, 1, 1, 4, 1, 38, ...] (Sloane's A030170). At 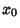 ,
, 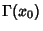 achieves the value 0.8856031944...
(Sloane's A030171), which has Continued Fraction [0, 1, 7, 1, 2, 1, 6, 1, 1, ...] (Sloane's A030172).
achieves the value 0.8856031944...
(Sloane's A030171), which has Continued Fraction [0, 1, 7, 1, 2, 1, 6, 1, 1, ...] (Sloane's A030172).
The Euler limit form is
so
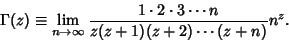 |
(20) |
The Lanczos Approximation for 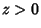 is
is
![\begin{displaymath}
\Gamma(z+1)=(z+\gamma+{\textstyle{1\over 2}})^{z+1/2}e^{z+\g...
...er z+1}+{c_2\over z+2}+\ldots+{c_n\over z+n}+\epsilon}\right].
\end{displaymath}](g_247.gif) |
(21) |
The complete gamma function 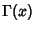 can be generalized to the incomplete gamma function
can be generalized to the incomplete gamma function  such
that
such
that
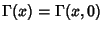 . The gamma function satisfies the recurrence relations
. The gamma function satisfies the recurrence relations
Additional identities are
For integral arguments, the first few values are 1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, ...
(Sloane's A000142). For half integral arguments,
In general, for 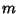 a Positive Integer
a Positive Integer  , 2, ...
, 2, ...
For
![$\Re[x]=-{1\over 2}$](g_278.gif) ,
,
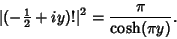 |
(34) |
Gamma functions of argument 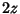 can be expressed using the Legendre Duplication Formula
can be expressed using the Legendre Duplication Formula
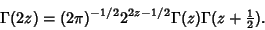 |
(35) |
Gamma functions of argument 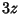 can be expressed using a triplication Formula
can be expressed using a triplication Formula
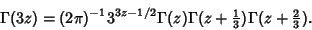 |
(36) |
The general result is the Gauss Multiplication Formula
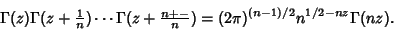 |
(37) |
The gamma function is also related to the Riemann Zeta Function 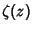 by
by
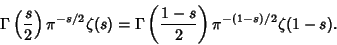 |
(38) |
Borwein and Zucker (1992) give a variety of identities relating gamma functions to square roots and Elliptic Integral
Singular Values 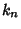 , i.e., Moduli
, i.e., Moduli 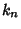 such that
such that
 |
(39) |
where 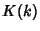 is a complete Elliptic Integral of the First Kind and
is a complete Elliptic Integral of the First Kind and
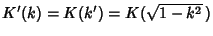 is the complementary
integral.
is the complementary
integral.
![$\quad \Gamma({\textstyle{1\over 3}})=2^{7/9}3^{-1/12}\pi^{1/3}[K(k_3)]^{1/3}$](g_291.gif)
|
(40) |
![$\quad \Gamma({\textstyle{1\over 4}})=2\pi^{1/4}[K(k_1)]^{1/2}$](g_292.gif)
|
(41) |
![$\quad \Gamma({\textstyle{1\over 6}})=2^{-1/3}3^{1/2}\pi^{-1/2}[\Gamma({\textstyle{1\over 3}})]^2$](g_293.gif)
|
(42) |
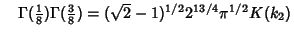
|
(43) |
![$\quad {\Gamma({\textstyle{1\over 8}})\over\Gamma({\textstyle{3\over 8}})}=2(\sqrt{2}+1)^{1/2}\pi^{-1/4}[K(k_1)]^{1/2}$](g_295.gif)
|
(44) |

|
(45) |
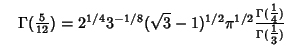
|
(46) |

|
(47) |
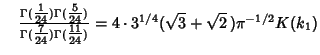
|
(48) |

|
(49) |
![$\quad \Gamma({\textstyle{1\over 24}})\Gamma({\textstyle{5\over 25}})\Gamma({\te...
...11\over 24}}) = 384(\sqrt{2}+1)(\sqrt{3}-\sqrt{2}\,)(2-\sqrt{3}\,)\pi[K(k_6)]^2$](g_301.gif)
|
(50) |
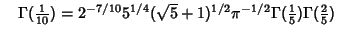
|
(51) |
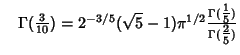
|
(52) |
![$\quad {\Gamma({\textstyle{1\over 15}})\Gamma({\textstyle{4\over 15}})\Gamma({\t...
...^{1/2}5^{1/6}\sin({\textstyle{2\over 15}}\pi)[\Gamma({\textstyle{1\over 3}})]^2$](g_304.gif)
|
(53) |
![$\quad {\Gamma({\textstyle{1\over 15}})\Gamma({\textstyle{2\over 15}})\Gamma({\t...
...\over 5}}\pi)\sin({\textstyle{4\over 15}}\pi)[\Gamma({\textstyle{1\over 5}})]^2$](g_305.gif)
|
(54) |
![$\quad {\Gamma({\textstyle{2\over 15}})\Gamma({\textstyle{4\over 15}})\Gamma({\t...
...^{1/2}[\Gamma({\textstyle{2\over 5}})]^2\over \sin({\textstyle{4\over 15}}\pi)}$](g_306.gif)
|
(55) |
![$\quad {\Gamma({\textstyle{1\over 15}})\Gamma({\textstyle{2\over 15}})\Gamma({\t...
...yle{7\over 15}})} = 60(\sqrt{5}-1)\sin({\textstyle{7\over 15}}\pi)[K(k_{15})]^2$](g_307.gif)
|
(56) |
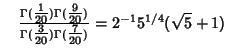
|
(57) |
![$\quad {\Gamma({\textstyle{1\over 20}})\Gamma({\textstyle{3\over 20}})\over\Gamm...
...over 20}}\pi)\sin({\textstyle{9\over 20}}\pi)[\Gamma({\textstyle{1\over 5}})]^2$](g_309.gif)
|
(58) |
![$\quad {\Gamma({\textstyle{1\over 20}})\Gamma({\textstyle{7\over 20}})\over\Gamm...
...over 20}}\pi)\sin({\textstyle{9\over 20}}\pi)[\Gamma({\textstyle{2\over 5}})]^2$](g_310.gif)
|
(59) |
![$\quad \Gamma({\textstyle{1\over 20}})\Gamma({\textstyle{3\over 20}})\Gamma({\te...
...over 20}})\Gamma({\textstyle{9\over 20}}) = 160(\sqrt{5}-2)^{1/2}\pi[K(k_5)]^2.$](g_311.gif)
|
(60) |
A few curious identities include
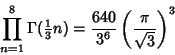 |
(61) |
![\begin{displaymath}
{[\Gamma({\textstyle{1\over 4}})]^4\over 16\pi^2}={3^2\over 3^2-1} {5^2-1\over 5^2} {7^2\over 7^2-1} \cdots
\end{displaymath}](g_313.gif) |
(62) |
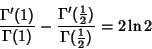 |
(63) |
(Magnus and Oberhettinger 1949, p. 1). Ramanujan also gave a number of fascinating identities:
![\begin{displaymath}
{\Gamma^2(n+1)\over\Gamma(n+xi+1)\Gamma(n-xi+1)}=\prod_{k=1}^\infty\left[{1+{x^2\over(n+k)^2}}\right]
\end{displaymath}](g_315.gif) |
(64) |
![\begin{displaymath}
\phi(m,n)\phi(n,m)={\Gamma^3(m+1)\Gamma^3(n+1)\over\Gamma(2m...
...h[\pi(m+n)\sqrt{3}\,]-\cos[\pi(m-n)]\over 2\pi^2(m^2+mn+n^2)},
\end{displaymath}](g_316.gif) |
(65) |
where
![\begin{displaymath}
\phi(m,n)\equiv\prod_{k=1}^\infty\left[{1+\left({m+n\over k+m}\right)^3}\right],
\end{displaymath}](g_317.gif) |
(66) |
![\begin{displaymath}
\prod_{k=1}^\infty\left[{1+\left({n\over k}\right)^3}\right]...
...)]}{\cosh(\pi n\sqrt{3}\,)-\cos(\pi n)\over 2^{n+2}\pi^{3/2}n}
\end{displaymath}](g_318.gif) |
(67) |
(Berndt 1994).
The following Asymptotic Series is occasionally useful in probability theory (e.g., the 1-D Random
Walk):
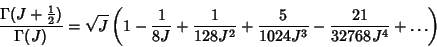 |
(68) |
(Graham et al. 1994). This series also gives a nice asymptotic generalization of Stirling Numbers of the First
Kind to fractional values.
It has long been known that
 is Transcendental (Davis 1959), as is
is Transcendental (Davis 1959), as is
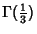 (Le Lionnais 1983), and Chudnovsky has apparently recently proved that
(Le Lionnais 1983), and Chudnovsky has apparently recently proved that
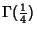 is itself Transcendental.
is itself Transcendental.
The upper incomplete gamma function is given by
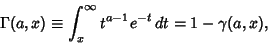 |
(69) |
where 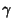 is the lower incomplete gamma function. For
is the lower incomplete gamma function. For 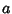 an Integer
an Integer 
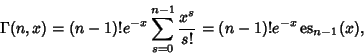 |
(70) |
where es is the Exponential Sum Function. The lower incomplete gamma function is given by
where
 is the Confluent Hypergeometric Function of the First Kind. For
is the Confluent Hypergeometric Function of the First Kind. For 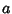 an Integer
an Integer  ,
,
The function 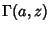 is denoted Gamma[a,z] and the function
is denoted Gamma[a,z] and the function 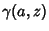 is denoted Gamma[a,0,z]
in Mathematica
is denoted Gamma[a,0,z]
in Mathematica
 (Wolfram Research, Champaign, IL).
(Wolfram Research, Champaign, IL).
See also Digamma Function, Double Gamma Function, Fransén-Robinson Constant G-Function, Gauss Multiplication Formula, Lambda Function, Legendre Duplication
Formula, Mu Function, Nu Function, Pearson's Function, Polygamma Function, Regularized
Gamma Function, Stirling's Series
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Gamma (Factorial) Function'' and ``Incomplete Gamma Function.'' §6.1
and 6.5 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 255-258 and 260-263, 1972.
Arfken, G. ``The Gamma Function (Factorial Function).'' Ch. 10 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 339-341 and 539-572, 1985.
Artin, E. The Gamma Function. New York: Holt, Rinehart, and Winston, 1964.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 334-342, 1994.
Borwein, J. M. and Zucker, I. J. ``Elliptic Integral Evaluation of the Gamma Function at Rational Values of Small
Denominator.'' IMA J. Numerical Analysis 12, 519-526, 1992.
Davis, H. T. Tables of the Higher Mathematical Functions. Bloomington, IN: Principia Press, 1933.
Davis, P. J. ``Leonhard Euler's Integral: A Historical Profile of the Gamma Function.'' Amer. Math. Monthly
66, 849-869, 1959.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/fran/fran.html
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Answer to problem 9.60 in
Concrete Mathematics: A Foundation for Computer Science. Reading, MA: Addison-Wesley, 1994.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 46, 1983.
Magnus, W. and Oberhettinger, F. Formulas and Theorems for the Special Functions of Mathematical Physics.
New York: Chelsea, 1949.
Nielsen, N. Handbuch der Theorie der Gammafunktion. New York: Chelsea, 1965.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Gamma Function, Beta Function, Factorials,
Binomial Coefficients'' and ``Incomplete Gamma Function, Error Function, Chi-Square Probability Function, Cumulative Poisson Function.''
§6.1 and 6.2 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge
University Press, pp. 206-209 and 209-214, 1992.
Sloane, N. J. A. Sequences
A030169,
A030170,
A030171,
A030172, and
A000142/M1675
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
Spanier, J. and Oldham, K. B. ``The Gamma Function 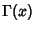 '' and ``The Incomplete Gamma
'' and ``The Incomplete Gamma
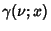 and Related Functions.''
Chs. 43 and 45 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 411-421 and 435-443, 1987.
and Related Functions.''
Chs. 43 and 45 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 411-421 and 435-443, 1987.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University
Press, 1990.
© 1996-9 Eric W. Weisstein
1999-05-25

![]() ,
, ![]() ,
, ![]() , ....
It can be defined as a Definite Integral for
, ....
It can be defined as a Definite Integral for ![]() (Euler's integral form)
(Euler's integral form)
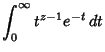
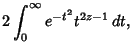

![$\displaystyle [-t^{x-1}e^{-t}]^\infty_0 + \int^\infty_0 (x-1)t^{x-2}e^{-t}\,dt$](g_202.gif)
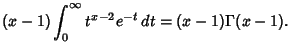
![\begin{displaymath}
\Gamma(z) \equiv \left[{ze^{\gamma z}\prod_{r=1}^\infty \left({1 + {z\over r}}\right)e^{-z/r}}\right]^{-1},
\end{displaymath}](g_209.gif)
![\begin{displaymath}
\Gamma(z)={1\over z}\mathop{\rm exp}\nolimits \left[{\sum_{k=1}^\infty {(-1)^k s_k\over k} x^k}\right],
\end{displaymath}](g_210.gif)
![\begin{displaymath}
-\ln[\Gamma(z)]=\ln z+\gamma z+\sum_{n=1}^\infty \left[{\ln\left({1+{z\over n}}\right)-{z\over n}}\right].
\end{displaymath}](g_217.gif)
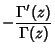
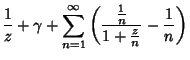
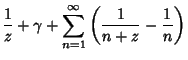
![$\displaystyle -\Gamma(z)\left[{{1\over z}+\gamma+\sum_{n=1}^\infty \left({{1\over n+z}-{1\over n}}\right)}\right]$](g_222.gif)
![$\displaystyle -\Gamma(1)-\left\{{1+\gamma+\left[{({\textstyle{1\over 2}}-1)+({\...
...over 2}})+\ldots+\left({{1\over n+1}-{1\over n}}\right)+\ldots}\right]}\right\}$](g_225.gif)
![$\displaystyle -\Gamma(n)\left\{{{1\over n}+\gamma+\left[{\left({{1\over 1+n}-1}...
...\over 2}}\right)+\left({{1\over 3+n}-{1\over 3}}\right)+\ldots}\right]}\right\}$](g_228.gif)
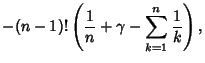
![]() of
of ![]() for Real Positive
for Real Positive ![]() is achieved when
is achieved when
![$\displaystyle z\left[{\,\lim_{m\to\infty} e^{(1+1/2+\ldots+1/m-\ln m)z}}\right]...
...fty} \prod_{n=1}^m \left\{{\left({1+{z\over n}}\right)e^{-z/n}}\right\}}\right]$](g_243.gif)
![$\displaystyle {1\over z}\prod_{n=1}^\infty \left[{\left({1+{1\over n}}\right)^z\left({1+{z\over n}}\right)^{-1}}\right],$](g_244.gif)
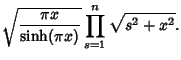
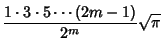

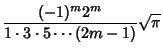

![]() , i.e., Moduli
, i.e., Moduli ![]() such that
such that
![$\quad {\Gamma({\textstyle{1\over 8}})\over\Gamma({\textstyle{3\over 8}})}=2(\sqrt{2}+1)^{1/2}\pi^{-1/4}[K(k_1)]^{1/2}$](g_295.gif)
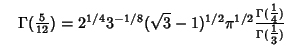

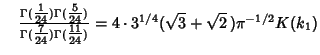
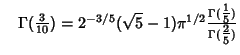
![$\quad {\Gamma({\textstyle{1\over 15}})\Gamma({\textstyle{4\over 15}})\Gamma({\t...
...^{1/2}5^{1/6}\sin({\textstyle{2\over 15}}\pi)[\Gamma({\textstyle{1\over 3}})]^2$](g_304.gif)
![$\quad {\Gamma({\textstyle{1\over 15}})\Gamma({\textstyle{2\over 15}})\Gamma({\t...
...\over 5}}\pi)\sin({\textstyle{4\over 15}}\pi)[\Gamma({\textstyle{1\over 5}})]^2$](g_305.gif)
![$\quad {\Gamma({\textstyle{2\over 15}})\Gamma({\textstyle{4\over 15}})\Gamma({\t...
...^{1/2}[\Gamma({\textstyle{2\over 5}})]^2\over \sin({\textstyle{4\over 15}}\pi)}$](g_306.gif)
![$\quad {\Gamma({\textstyle{1\over 15}})\Gamma({\textstyle{2\over 15}})\Gamma({\t...
...yle{7\over 15}})} = 60(\sqrt{5}-1)\sin({\textstyle{7\over 15}}\pi)[K(k_{15})]^2$](g_307.gif)
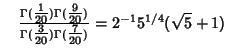
![$\quad {\Gamma({\textstyle{1\over 20}})\Gamma({\textstyle{3\over 20}})\over\Gamm...
...over 20}}\pi)\sin({\textstyle{9\over 20}}\pi)[\Gamma({\textstyle{1\over 5}})]^2$](g_309.gif)
![$\quad {\Gamma({\textstyle{1\over 20}})\Gamma({\textstyle{7\over 20}})\over\Gamm...
...over 20}}\pi)\sin({\textstyle{9\over 20}}\pi)[\Gamma({\textstyle{2\over 5}})]^2$](g_310.gif)
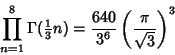
![\begin{displaymath}
{\Gamma^2(n+1)\over\Gamma(n+xi+1)\Gamma(n-xi+1)}=\prod_{k=1}^\infty\left[{1+{x^2\over(n+k)^2}}\right]
\end{displaymath}](g_315.gif)
![\begin{displaymath}
\phi(m,n)\equiv\prod_{k=1}^\infty\left[{1+\left({m+n\over k+m}\right)^3}\right],
\end{displaymath}](g_317.gif)
![\begin{displaymath}
\prod_{k=1}^\infty\left[{1+\left({n\over k}\right)^3}\right]...
...)]}{\cosh(\pi n\sqrt{3}\,)-\cos(\pi n)\over 2^{n+2}\pi^{3/2}n}
\end{displaymath}](g_318.gif)
![]() is Transcendental (Davis 1959), as is
is Transcendental (Davis 1959), as is
![]() (Le Lionnais 1983), and Chudnovsky has apparently recently proved that
(Le Lionnais 1983), and Chudnovsky has apparently recently proved that
![]() is itself Transcendental.
is itself Transcendental.
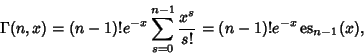

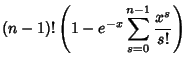
![]() '' and ``The Incomplete Gamma
'' and ``The Incomplete Gamma
![]() and Related Functions.''
Chs. 43 and 45 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 411-421 and 435-443, 1987.
and Related Functions.''
Chs. 43 and 45 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 411-421 and 435-443, 1987.