Confluent Hypergeometric Function of the First Kind

The confluent hypergeometric function is a degenerate form the Hypergeometric Function ${}_2F_1(a,b;c;z)$ which arises as a solution the Confluent Hypergeometric Differential Equation. It is commonly denoted ${}_1F_1(a;b;z)$, $M(a,b,z)$, or $\Phi(a;b;z)$, and is also known as Kummer's Function of the first kind. An alternate form of the solution to the Confluent Hypergeometric Differential Equation is known as the Whittaker Function.

The confluent hypergeometric function has a Hypergeometric Series given by

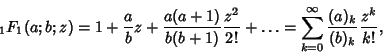$${}_1F_1(a;b;z)=1+{a\over b}z+{a(a+1)\over b(b+1)} {z^2\over ... ... \ldots = \sum_{k=0}^\infty {(a)_k\over (b)_k} {z^k\over k!},$$ (1)

where $(a)_k$ and $(b)_k$ are Pochhammer Symbols. If $a$ and $b$ are Integers, $a<0$, and either $b>0$ or $b<a$, then the series yields a Polynomial with a finite number of terms. If $b$ is an Integer $\leq 0$, then ${}_1F_1(a;b;z)$ is undefined. The confluent hypergeometric function also has an integral representation

$${}_1F_1(a;b;z) = {\Gamma(b)\over\Gamma(b-a)\Gamma(a)} \int_0^1 e^{zt}t^{a-1}(1-t)^{b-a-1}\,dt$$ (2)

(Abramowitz and Stegun 1972, p. 505).

Bessel Functions, the Error Function, the incomplete Gamma Function, Hermite Polynomial, Laguerre Polynomial, as well as other are all special cases of this function (Abramowitz and Stegun 1972, p. 509).

Kummer's Second Formula gives

$${}_1F_1({\textstyle{1\over 2}}+m;2m+1;z) = M_{0,m}(z)$$

$$= z^{m+1/2}\left[{1+\sum_{p=1}^\infty {z^{2p}\over 2^{4p} p!(m+1)(m+2)\cdots (m+p)}}\right],$$ (3)

where ${}_1F_1(a;b;z)$ is the Confluent Hypergeometric Function and $m\not= -1/2$, $-1$, $-3/2$, ....

See also Confluent Hypergeometric Differential Equation, Confluent Hypergeometric Function of the Second Kind, Confluent Hypergeometric Limit Function, Generalized Hypergeometric Function, Heine Hypergeometric Series, Hypergeometric Function, Hypergeometric Series, Kummer's Formulas, Weber-Sonine Formula, Whittaker Function

References

Abramowitz, M. and Stegun, C. A. (Eds.). ``Confluent Hypergeometric Functions.'' Ch. 13 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 503-515, 1972.

Arfken, G. ``Confluent Hypergeometric Functions.'' §13.6 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 753-758, 1985.

Iyanaga, S. and Kawada, Y. (Eds.). ``Hypergeometric Function of Confluent Type.'' Appendix A, Table 19.I in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1469, 1980.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 551-554 and 604-605, 1953.

Slater, L. J. Confluent Hypergeometric Functions. Cambridge, England: Cambridge University Press, 1960.

Spanier, J. and Oldham, K. B. ``The Kummer Function $M(a;c;x)$.'' Ch. 47 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 459-469, 1987.