|
|
|
The Asymptotic Series for the Gamma Function is given by
| (1) |
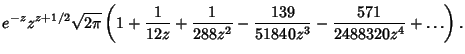 |
(2) |
 |
(3) | ||
| (4) |
See also Bernoulli Number, K-Function, Stirling's Approximation
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 257, 1972.
Arfken, G. ``Stirling's Series.'' §10.3 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 555-559, 1985.
Conway, J. H. and Guy, R. K. ``Stirling's Formula.'' In The Book of Numbers.
New York: Springer-Verlag, pp. 260-261, 1996.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York:
McGraw-Hill, p. 443, 1953.
Sloane, N. J. A. Sequences
A001163/M5400
and A001164/M4878
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.