|
|
|
The number of ways of partitioning a set of ![]() elements into
elements into ![]() nonempty Sets (i.e.,
nonempty Sets (i.e., ![]() Blocks), also called a Stirling Set Number. For example, the Set
Blocks), also called a Stirling Set Number. For example, the Set ![]() can be partitioned into
three Subsets in one way:
can be partitioned into
three Subsets in one way:
![]() ; into two Subsets in three ways:
; into two Subsets in three ways:
![]() ,
,
![]() , and
, and
![]() ; and into one Subset in one way:
; and into one Subset in one way:
![]() .
.
The Stirling numbers of the second kind are denoted ![]() ,
, ![]() ,
, ![]() , or
, or
![]() , so the Stirling numbers of the second kind for three elements are
, so the Stirling numbers of the second kind for three elements are
| (1) | |||
| (2) | |||
| (3) |
| (4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The Stirling numbers of the second kind can be computed from the sum
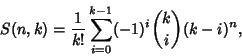 |
(5) |
 |
(6) |
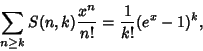 |
(7) |
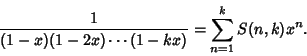 |
(8) |
The following diagrams (Dickau) illustrate the definition of the Stirling numbers of the second kind
![]() for
for ![]() and 4.
and 4.
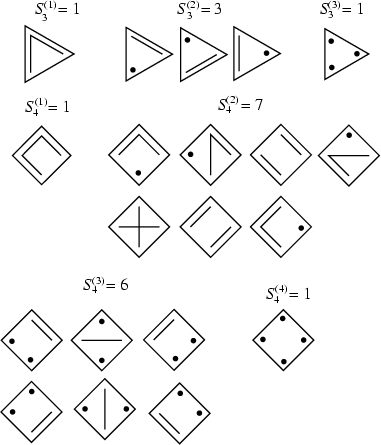
Stirling numbers of the second kind obey the Recurrence Relations
| (9) |
An identity involving Stirling numbers of the second kind is
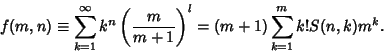 |
(10) |
See also Bell Number, Combination Lock, Lengyel's Constant, Minimal Cover, Stirling Number of the First Kind
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Stirling Numbers of the Second Kind.'' §24.1.4 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 824-825, 1972.
Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Boston, MA: Reidel, 1974.
Conway, J. H. and Guy, R. K. In The Book of Numbers. New York: Springer-Verlag, pp. 91-92, 1996.
Dickau, R. M. ``Stirling Numbers of the Second Kind.''
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed.
Reading, MA: Addison-Wesley, 1994.
Knuth, D. E. ``Two Notes on Notation.'' Amer. Math. Monthly 99, 403-422, 1992.
Riordan, J. An Introduction to Combinatorial Analysis. New York: Wiley, 1980.
Riordan, J. Combinatorial Identities. New York: Wiley, 1968.
Riskin, A. ``Problem 10231.'' Amer. Math. Monthly 102, 175-176, 1995.
Sloane, N. J. A. Sequence
A008277
in ``The On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
Stanley, R. P. Enumerative Combinatorics, Vol. 1. Cambridge, England: Cambridge University Press, 1997.
http://forum.swarthmore.edu/advanced/robertd/stirling2.html
|
|
|
© 1996-9 Eric W. Weisstein