Minimal Cover

A minimal cover is a Cover for which removal of one member destroys the covering property. Let $\mu(n,k)$ be the number of minimal covers of $\{1, \ldots, n\}$ with $k$ members. Then

$$\mu(n,k)={1\over k!} \sum_{m=k}^{\alpha_k} {2^k-k-1\choose m-k}m! s(n,m),$$

where ${n\choose k}$ is a Binomial Coefficient, $s(n,m)$ is a Stirling Number of the Second Kind, and

$$\alpha_k={\rm min}(n,2^k-1).$$

Special cases include $\mu(n,1)=1$ and $\mu(n,2)=s(n+1,3)$.

$n$	$k=1$	$k=2$	$k=3$	$k=4$	$k=5$	$k=6$	$k=7$
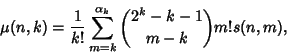
Sloane		Sloane's A000392	Sloane's A003468	Sloane's A016111
1	1
2	1	1
3	1	6	1
4	1	25	22	1
5	1	90	305	65	1
6	1	301	3410	2540	171	1
7	1	966	33621	77350	17066	420	1

See also Cover, Lew k-gram, Stirling Number of the Second Kind

References

Hearne, T. and Wagner, C. ``Minimal Covers of Finite Sets.'' Disc. Math. 5, 247-251, 1973.

Macula, A. J. ``Lewis Carroll and the Enumeration of Minimal Covers.'' Math. Mag. 68, 269-274, 1995.