|
|
|
The number of ways a Set of ![]() elements can be Partitioned into nonempty
Subsets is called a Bell Number and is denoted
elements can be Partitioned into nonempty
Subsets is called a Bell Number and is denoted ![]() . For example, there are five ways the
numbers
. For example, there are five ways the
numbers ![]() 1, 2, 3
1, 2, 3![]() can be partitioned:
can be partitioned:
![]() ,
,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() , so
, so ![]() .
. ![]() and the first few Bell
numbers for
and the first few Bell
numbers for ![]() , 2, ... are 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, ... (Sloane's A000110). Bell numbers are
closely related to Catalan Numbers.
, 2, ... are 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, ... (Sloane's A000110). Bell numbers are
closely related to Catalan Numbers.
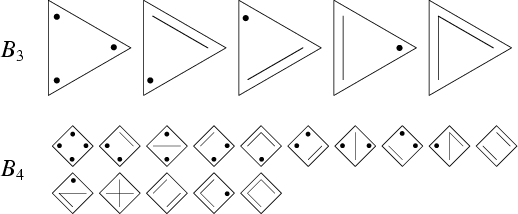
The diagram below shows the constructions giving ![]() and
and ![]() , with line segments representing elements in the
same Subset and dots representing subsets containing a single element (Dickau).
, with line segments representing elements in the
same Subset and dots representing subsets containing a single element (Dickau).
The Integers ![]() can be defined by the sum
can be defined by the sum
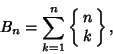 |
(1) |
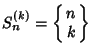 is a
Stirling Number of the Second Kind, or by the generating function
is a
Stirling Number of the Second Kind, or by the generating function
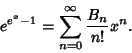 |
(2) |
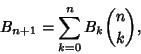 |
(3) |
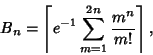 |
(4) |
The Bell number ![]() is also equal to
is also equal to ![]() , where
, where ![]() is a Bell Polynomial. Dobinski's
Formula gives the
is a Bell Polynomial. Dobinski's
Formula gives the ![]() th Bell number
th Bell number
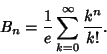 |
(5) |
| (6) |
| (7) |
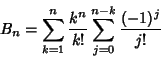 |
(8) |
| (9) |
Touchard's Congruence states
| (10) |
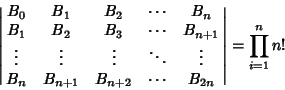 |
(11) |
See also Bell Polynomial, Bell Triangle, Dobinski's Formula, Stirling Number of the Second Kind, Touchard's Congruence
References
Bell, E. T. ``Exponential Numbers.'' Amer. Math. Monthly 41, 411-419, 1934.
Comtet, L. Advanced Combinatorics. Dordrecht, Netherlands: Reidel, 1974.
Conway, J. H. and Guy, R. K. In The Book of Numbers. New York: Springer-Verlag, pp. 91-94, 1996.
de Bruijn, N. G. Asymptotic Methods in Analysis. New York: Dover, pp. 102-109, 1958.
Dickau, R. M. ``Bell Number Diagrams.''
http://forum.swarthmore.edu/advanced/robertd/bell.html.
Gardner, M. ``The Tinkly Temple Bells.'' Ch. 2 in
Fractal Music, Hypercards, and More Mathematical Recreations from Scientific American Magazine.
New York: W. H. Freeman, 1992.
Gould, H. W. Bell & Catalan Numbers: Research Bibliography of Two Special Number Sequences, 6th ed.
Morgantown, WV: Math Monongliae, 1985.
Lenard, A. In
Fractal Music, Hypercards, and More Mathematical Recreations from Scientific American Magazine. (M. Gardner).
New York: W. H. Freeman, pp. 35-36, 1992.
Levine, J. and Dalton, R. E. ``Minimum Periods, Modulo
Lovász, L. Combinatorial Problems and Exercises, 2nd ed. Amsterdam, Netherlands:
North-Holland, 1993.
Pitman, J. ``Some Probabilistic Aspects of Set Partitions.'' Amer. Math. Monthly 104, 201-209, 1997.
Rota, G.-C. ``The Number of Partitions of a Set.'' Amer. Math. Monthly 71, 498-504, 1964.
Sloane, N. J. A. Sequence
A000110/M1484
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
![]() , of First Order Bell Exponential Integrals.''
Math. Comput. 16, 416-423, 1962.
, of First Order Bell Exponential Integrals.''
Math. Comput. 16, 416-423, 1962.
|
|
|
© 1996-9 Eric W. Weisstein