|
|
|
Gives the ![]() th Bell Number,
th Bell Number,
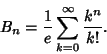 |
(1) |
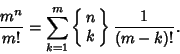 |
(2) |
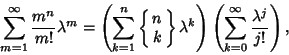 |
(3) |
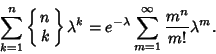 |
(4) |
References
Berge, C. Principles of Combinatorics. New York: Academic Press, 1971.
Chen, B. and Yeh, Y.-N. ``Some Explanations of Dobinski's Formula.'' Studies Appl. Math. 92, 191-199,
1994.
Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Boston, MA: Reidel, 1974.
Dobinski, G. ``Summierung der Reihe
Foata, D. La série génératrice exponentielle dans les problèmes d'énumération. Vol. 54 of
Séminaire de Mathématiques supérieures. Montréal, Canada: Presses de l'Université de Montréal, 1974.
Lupas, A. ``Dobinski-Type Formula for Binomial Polynomials.'' Stud. Univ. Babes-Bolyai Math. 33, 30-44, 1988.
Pitman, J. ``Some Probabilistic Aspects of Set Partitions.'' Amer. Math. Monthly 104, 201-209, 1997.
Roman, S. The Umbral Calculus. New York: Academic Press, 1984.
Rota, G.-C. ``The Number of Partitions of a Set.'' Amer. Math. Monthly 71, 498-504, 1964.
Wilf, H. Generatingfunctionology, 2nd ed. San Diego, CA: Academic Press, 1990.
![]() für
für ![]() , 2, 3, 4, 5, ....''
Grunert Archiv (Arch. Math. Phys.) 61, 333-336, 1877.
, 2, 3, 4, 5, ....''
Grunert Archiv (Arch. Math. Phys.) 61, 333-336, 1877.