|
|
|
For the ![]() th Prime
th Prime ![]() ,
,
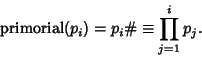
![]() is Prime for Primes
is Prime for Primes ![]() , 5, 11, 41, 89, 317, 337, 991, 1873, 2053, 2377, 4093, 4297, ... (Sloane's A014563;
Guy 1994), or
, 5, 11, 41, 89, 317, 337, 991, 1873, 2053, 2377, 4093, 4297, ... (Sloane's A014563;
Guy 1994), or ![]() for
for ![]() , 3, 5, 13, 24, 66, 68, 167, 287, 310, 352, 564, 590, ....
, 3, 5, 13, 24, 66, 68, 167, 287, 310, 352, 564, 590, .... ![]() is known to be Prime for
the Primes
is known to be Prime for
the Primes ![]() , 3, 5, 7, 11, 31, 379, 1019, 1021, 2657, 3229, 4547, 4787, 11549, ... (Sloane's A005234; Guy 1994, Mudge
1997), or
, 3, 5, 7, 11, 31, 379, 1019, 1021, 2657, 3229, 4547, 4787, 11549, ... (Sloane's A005234; Guy 1994, Mudge
1997), or ![]() for
for ![]() , 2, 3, 4, 5, 11, 75, 171, 172, 384, 457, 616, 643, 1391, ... (Sloane's A014545). Both forms have been tested to
, 2, 3, 4, 5, 11, 75, 171, 172, 384, 457, 616, 643, 1391, ... (Sloane's A014545). Both forms have been tested to
![]() (Caldwell 1995). It is not known if there are an infinite number of Primes for which
(Caldwell 1995). It is not known if there are an infinite number of Primes for which ![]() is Prime or
Composite (Ribenboim 1989).
is Prime or
Composite (Ribenboim 1989).
See also Factorial, Fortunate Prime, Prime Sum Smarandache Near-to-Primorial Function, Twin Peaks
References
Borning, A. ``Some Results for
Buhler, J. P.; Crandall, R. E.; and Penk, M. A. ``Primes of the form
Caldwell, C. ``On The Primality of
Dubner, H. ``Factorial and Primorial Primes.'' J. Rec. Math. 19, 197-203, 1987.
Dubner, H. ``A New Primorial Prime.'' J. Rec. Math. 21, 276, 1989.
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 7-8, 1994.
Leyland, P.
ftp://sable.ox.ac.uk/pub/math/factors/primorial-.Z and
ftp://sable.ox.ac.uk/pub/math/factors/primorial+.Z.
Mudge, M. ``Not Numerology but Numeralogy!'' Personal Computer World, 279-280, 1997.
Ribenboim, P. The Book of Prime Number Records, 2nd ed. New York: Springer-Verlag, p. 4, 1989.
Sloane, N. J. A. Sequences A002110/M1691, A005234/M0669, A014545, and A014563 in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
Temper, M. ``On the Primality of
![]() and
and
![]() .'' Math. Comput. 26, 567-570, 1972.
.'' Math. Comput. 26, 567-570, 1972.
![]() and
and
![]() .'' Math. Comput. 38, 639-643, 1982.
.'' Math. Comput. 38, 639-643, 1982.
![]() and
and
![]() .'' Math. Comput. 64, 889-890, 1995.
.'' Math. Comput. 64, 889-890, 1995.
![]() and
and
![]() .'' Math. Comput. 34, 303-304, 1980.
.'' Math. Comput. 34, 303-304, 1980.
|
|
|
© 1996-9 Eric W. Weisstein