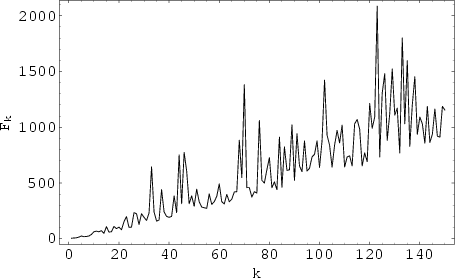
Let
where 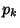 is the
is the  th Prime and
th Prime and 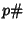 is the Primorial, and let
is the Primorial, and let 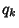 be the Next Prime (i.e., the
smallest Prime greater than
be the Next Prime (i.e., the
smallest Prime greater than 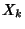 ),
),
where 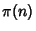 is the Prime Counting Function. Then R. F. Fortune conjectured that
is the Prime Counting Function. Then R. F. Fortune conjectured that
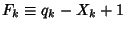 is
Prime for all
is
Prime for all  . The first values of
. The first values of 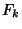 are 3, 5, 7, 13, 23, 17, 19, 23, ... (Sloane's A005235), and all known
values of
are 3, 5, 7, 13, 23, 17, 19, 23, ... (Sloane's A005235), and all known
values of 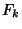 are indeed Prime (Guy 1994). The indices of these primes are 2, 3, 4, 6, 9, 7, 8, 9, 12, 18, .... In
numerical order with duplicates removed, the Fortunate primes are 3, 5, 7, 13, 17, 19, 23, 37, 47, 59, 61, 67, 71, 79, 89, ...
(Sloane's A046066).
are indeed Prime (Guy 1994). The indices of these primes are 2, 3, 4, 6, 9, 7, 8, 9, 12, 18, .... In
numerical order with duplicates removed, the Fortunate primes are 3, 5, 7, 13, 17, 19, 23, 37, 47, 59, 61, 67, 71, 79, 89, ...
(Sloane's A046066).
See also Andrica's Conjecture, Primorial
References
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 7, 1994.
Sloane, N. J. A. Sequences
A046066 and
A005235/M2418
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
© 1996-9 Eric W. Weisstein
1999-05-26