|
|
|
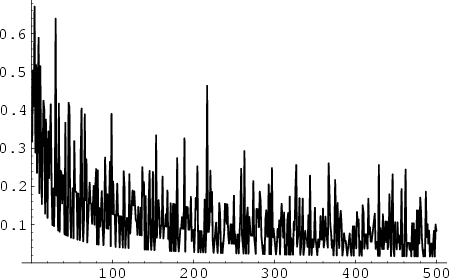
Andrica's conjecture states that, for ![]() the
the ![]() th Prime Number, the Inequality
th Prime Number, the Inequality
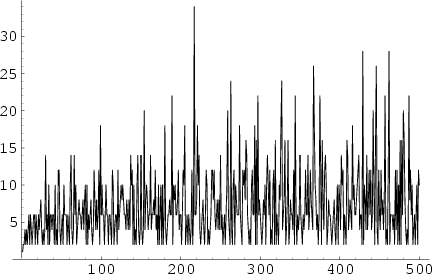
![]() bears a strong resemblance to the Prime Difference Function, plotted above, the first few values of
which are 1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, ... (Sloane's A001223).
bears a strong resemblance to the Prime Difference Function, plotted above, the first few values of
which are 1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, ... (Sloane's A001223).
See also Brocard's Conjecture, Good Prime, Fortunate Prime, Pólya Conjecture, Prime Difference Function, Twin Peaks
References
Golomb, S. W. ``Problem E2506: Limits of Differences of Square Roots.'' Amer. Math. Monthly 83, 60-61, 1976.
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 21, 1994.
Rivera, C. ``Problems & Puzzles (Conjectures): Andrica's Conjecture.''
http://www.sci.net.mx/~crivera/conjectures/conj_008.htm.
Sloane, N. J. A. Sequence
A001223/M0296
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.