|
|
|
A constant related to the Twin Primes Constant which appears in the Formula for the sum of inverse Primes
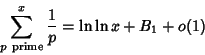 |
(1) |
![\begin{displaymath}
B_1=\gamma+\sum_{p{\rm\ prime}} \left[{\ln(1-p^{-1})+{1\over p}}\right]\approx 0.261497.
\end{displaymath}](m_1038.gif) |
(2) |
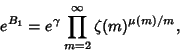 |
(3) |
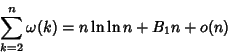 |
(4) |
The related constant
![\begin{displaymath}
B_2=\gamma+\sum_{p{\rm\ prime}} \left[{\ln(1-p^{-1})+{1\over p-1}}\right]\approx 1.034653
\end{displaymath}](m_1043.gif) |
(5) |
 |
(6) |
See also Brun's Constant, Prime Number, Twin Primes Constant
References
Flajolet, P. and Vardi, I. ``Zeta Function Expansions of Classical Constants.'' Unpublished manuscript. 1996.
http://pauillac.inria.fr/algo/flajolet/Publications/landau.ps.
Hardy, G. H. and Weight, E. M. An Introduction to the Theory of Numbers, 5th ed.
Oxford, England: Oxford University Press, pp. 351 and 355, 1979.