|
|
|

The number of distinct prime factors of a number ![]() is denoted
is denoted ![]() . The first few values for
. The first few values for ![]() , 2, ... are
0, 1, 1, 1, 1, 2, 1, 1, 1, 2, 1, 2, 1, 2, 2, 1, 1, 2, 1, 2, ... (Sloane's A001221). The first few values of the
Summatory Function
, 2, ... are
0, 1, 1, 1, 1, 2, 1, 1, 1, 2, 1, 2, 1, 2, 2, 1, 1, 2, 1, 2, ... (Sloane's A001221). The first few values of the
Summatory Function
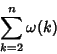
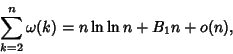
![\begin{displaymath}
\sum_{k=2}^n [\omega(k)]^2=n(\ln\ln n)^2+{\mathcal O}(n\ln\ln n).
\end{displaymath}](d2_1013.gif)
See also Divisor Function, Greatest Prime Factor, Hardy-Ramanujan Theorem, Heterogeneous Numbers, Least Prime Factor, Mertens Constant, Prime Factors
References
Hardy, G. H. and Wright, E. M. ``The Number of Prime Factors of
Sloane, N. J. A. Sequences
A013939 and
A001221/M0056
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
![]() '' and ``The Normal Order of
'' and ``The Normal Order of ![]() and
and ![]() .''
§22.10 and 22.11 in
An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 354-358, 1979.
.''
§22.10 and 22.11 in
An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 354-358, 1979.