For an Integer  , let
, let
 denote the Least Prime Factor of
denote the Least Prime Factor of 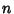 , i.e., the number
, i.e., the number 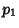 in
the factorization
in
the factorization
with  for
for  . For
. For 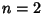 , 3, ..., the first few are 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, ...
(Sloane's A020639). The above plot of the least prime factor function can be seen to resemble a jagged terrain of mountains,
which leads to the appellation of ``Twin Peaks'' to a Pair of Integers
, 3, ..., the first few are 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, ...
(Sloane's A020639). The above plot of the least prime factor function can be seen to resemble a jagged terrain of mountains,
which leads to the appellation of ``Twin Peaks'' to a Pair of Integers 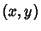 such that
such that
- 1.
 ,
,
- 2.
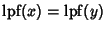 ,
,
- 3. For all
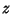 ,
, 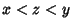 Implies
Implies
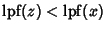 .
.
The least multiple prime factors for Squareful integers are 2, 2, 3, 2, 2, 3, 2, 2, 5, 3, 2, 2, 2,
... (Sloane's A046027).
See also Alladi-Grinstead Constant, Distinct Prime Factors, Erdös-Selfridge
Function, Factor, Greatest Prime Factor, Least Common Multiple, Mangoldt Function,
Prime Factors, Twin Peaks
References
Sloane, N. J. A.
A020639 and
A046027
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
© 1996-9 Eric W. Weisstein
1999-05-26

![]() , let
, let
![]() denote the Least Prime Factor of
denote the Least Prime Factor of ![]() , i.e., the number
, i.e., the number ![]() in
the factorization
in
the factorization