Let 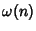 be the number of Distinct Prime Factors of
be the number of Distinct Prime Factors of 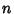 . If
. If 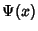 tends steadily to infinity with
tends steadily to infinity with 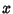 ,
then
,
then
for Almost All numbers  . ``Almost All'' means here the frequency of those Integers
. ``Almost All'' means here the frequency of those Integers 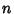 in the interval
in the interval 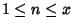 for which
for which
approaches 0 as 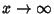 .
.
See also Distinct Prime Factors, Erdös-Kac Theorem
© 1996-9 Eric W. Weisstein
1999-05-25
![]() be the number of Distinct Prime Factors of
be the number of Distinct Prime Factors of ![]() . If
. If ![]() tends steadily to infinity with
tends steadily to infinity with ![]() ,
then
,
then