|
|
|
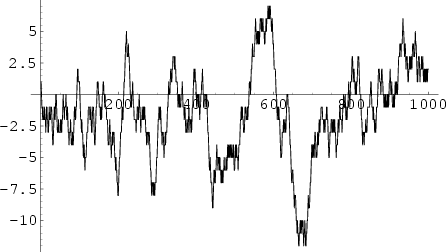
The summary function
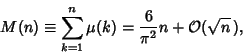
Mertens function obeys
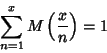
Lehman (1960) gives an algorithm for computing ![]() with
with
![]() operations,
while the Lagarias-Odlyzko (1987) algorithm for computing the Prime Counting Function
operations,
while the Lagarias-Odlyzko (1987) algorithm for computing the Prime Counting Function ![]() can be modified
to give
can be modified
to give ![]() in
in
![]() operations.
operations.
See also Mertens Conjecture, Möbius Function
References
Lagarias, J. and Odlyzko, A. ``Computing
Lehman, R. S. ``On Liouville's Function.'' Math. Comput. 14, 311-320, 1960.
Odlyzko, A. M. and te Riele, H. J. J. ``Disproof of the Mertens Conjecture.'' J. reine angew. Math. 357, 138-160, 1985.
Sloane, N. J. A. Sequences
A028442 and
A002321/M0102
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
![]() : An Analytic Method.'' J. Algorithms 8, 173-191, 1987.
: An Analytic Method.'' J. Algorithms 8, 173-191, 1987.