|
|
|
The function obtained by approximating the Riemann Weighted Prime-Power Counting Function ![]() in
in
 |
(1) |
 |
(2) | ||
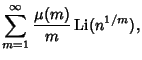 |
(3) |
| (4) |
See also Mangoldt Function, Prime Number Theorem, Riemann-Mangoldt Function, Riemann Zeta Function
References
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 144-145, 1996.
Riesel, H. and Göhl, G. ``Some Calculations Related to Riemann's Prime Number Formula.'' Math. Comput. 24, 969-983, 1970.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 28-29 and 362-372, 1991.