|
|
|
Primes for which Kummer's theorem on the unsolvability of Fermat's Last Theorem does not apply. An irregular
prime ![]() divides the Numerator of one of the Bernoulli Numbers
divides the Numerator of one of the Bernoulli Numbers ![]() ,
, ![]() , ...,
, ...,
![]() , as shown by Kummer in 1850. The Fermat Equation has no solutions for Regular Primes.
, as shown by Kummer in 1850. The Fermat Equation has no solutions for Regular Primes.
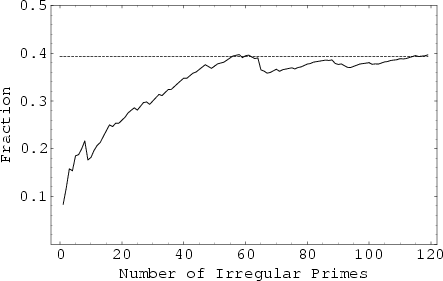
An Infinite number of irregular primes exist, as proven in 1915 by Jensen. The first few irregular primes are
37, 59, 67, 101, 103, 131, 149, 157, ... (Sloane's A000928). Of the 283,145 Primes less than ![]() , 111,597
(or 39.41%) are irregular. The conjectured Fraction is
, 111,597
(or 39.41%) are irregular. The conjectured Fraction is
![]() (Ribenboim 1996, p. 415).
(Ribenboim 1996, p. 415).
See also Bernoulli Number, Fermat's Last Theorem, Irregular Pair, Regular Prime
References
Buhler, J.; Crandall, R.; Ernvall, R.; and Metsänkylä, T. ``Irregular Primes and Cyclotomic Invariants to Four Million.''
Math. Comput. 60, 151-153, 1993.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press,
p. 202, 1979.
Johnson, W. ``Irregular Primes and Cyclotomic Invariants.'' Math. Comput. 29, 113-120, 1975.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 325-329 and 414-425, 1996.
Sloane, N. J. A. Sequence
A000928/M5260
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Stewart, C. L. ``A Note on the Fermat Equation.'' Mathematika 24, 130-132, 1977.