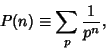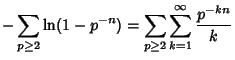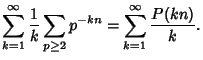The prime zeta function
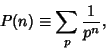 |
(1) |
where the sum is taken over Primes is a generalization of the Riemann Zeta Function
 |
(2) |
where the sum is over all integers. The prime zeta function can be expressed in terms of the Riemann Zeta Function
by
Inverting then gives
 |
(4) |
where 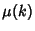 is the Möbius Function. The values for the first few integers starting with two are
is the Möbius Function. The values for the first few integers starting with two are
See also Möbius Function, Riemann Zeta Function, Zeta Function
References
Hardy, G. H. and Weight, E. M. An Introduction to the Theory of Numbers, 5th ed.
Oxford, England: Oxford University Press, pp. 355-356, 1979.
© 1996-9 Eric W. Weisstein
1999-05-26