|
|
|
A function satisfying certain properties which is computed as an Infinite Sum of Negative
Powers. The most commonly encountered zeta function is the Riemann Zeta Function,
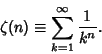
See also Dedekind Function, Dirichlet Beta Function, Dirichlet Eta Function, Dirichlet L-Series, Dirichlet Lambda Function, Epstein Zeta Function, Jacobi Zeta Function, Nint Zeta Function, Prime Zeta Function, Riemann Zeta Function
References
Ireland, K. and Rosen, M. ``The Zeta Function.'' Ch. 11 in
A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, pp. 151-171, 1990.