|
|
|
Series of the form
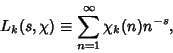 |
(1) |
 |
(2) |
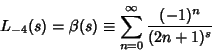 |
(3) |
| (4) |
Let ![]() or
or
![]() , where
, where ![]() are distinct Odd Primes. Then there are three possible types of
primitive
are distinct Odd Primes. Then there are three possible types of
primitive ![]() -series with Real Coefficients. The requirement of
Real Coefficients restricts the Character
to
-series with Real Coefficients. The requirement of
Real Coefficients restricts the Character
to
![]() for all
for all ![]() and
and ![]() . The three type are then
. The three type are then
| (5) |
| (6) |
| (7) |
The first few primitive Negative ![]() -series are
-series are ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() , ... (Sloane's A003657), corresponding to the negated discriminants of imaginary quadratic fields. The
first few primitive Positive
, ... (Sloane's A003657), corresponding to the negated discriminants of imaginary quadratic fields. The
first few primitive Positive ![]() -series are
-series are ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() , ... (Sloane's A046113).
, ... (Sloane's A046113).
The Kronecker Symbol is a Real Character modulo ![]() , and is
in fact essentially the only type of Real primitive Character
(Ayoub 1963). Therefore,
, and is
in fact essentially the only type of Real primitive Character
(Ayoub 1963). Therefore,
 |
(8) | ||
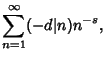 |
(9) |
| (10) | |||
| (11) |
| (12) | |||
| (13) | |||
| (14) | |||
| (15) | |||
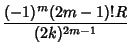 |
(16) | ||
 |
(17) |
| (18) |
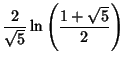 |
|||
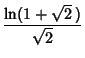 |
|||
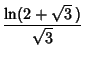 |
|||
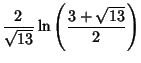 |
|||
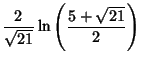 |
|||
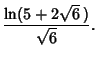 |
| (19) |
See also Dirichlet Beta Function, Dirichlet Eta Function
References
Ayoub, R. G. An Introduction to the Analytic Theory of Numbers. Providence, RI: Amer. Math. Soc., 1963.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, 1987.
Buell, D. A. ``Small Class Numbers and Extreme Values of
Ireland, K. and Rosen, M. ``Dirichlet
Sloane, N. J. A. Sequences
A046113 and
A003657/M2332
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Zucker, I. J. and Robertson, M. M. ``Some Properties of Dirichlet
![]() -Functions of Quadratic Fields.'' Math. Comput. 139, 786-796, 1977.
-Functions of Quadratic Fields.'' Math. Comput. 139, 786-796, 1977.
![]() -Functions.'' Ch. 16 in A Classical Introduction to Modern Number Theory, 2nd ed.
New York: Springer-Verlag, pp. 249-268, 1990.
-Functions.'' Ch. 16 in A Classical Introduction to Modern Number Theory, 2nd ed.
New York: Springer-Verlag, pp. 249-268, 1990.
![]() Weisstein, E. W. ``Class Numbers.'' Mathematica notebook ClassNumbers.m.
Weisstein, E. W. ``Class Numbers.'' Mathematica notebook ClassNumbers.m.
![]() -Series.'' J. Phys. A: Math. Gen. 9, 1207-1214, 1976.
-Series.'' J. Phys. A: Math. Gen. 9, 1207-1214, 1976.
|
|
|
© 1996-9 Eric W. Weisstein