|
|
|
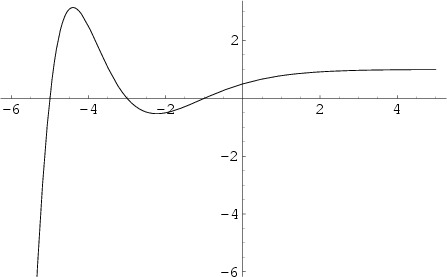

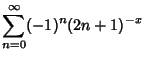 |
(1) | ||
| (2) |
| (3) |
| (4) |
| (5) |
Particular values for ![]() are
are
| (6) | |||
| (7) | |||
| (8) |
See also Catalan's Constant, Dirichlet Eta Function, Dirichlet Lambda Function, Hurwitz Zeta Function, Lerch Transcendent, Riemann Zeta Function, Zeta Function
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 807-808, 1972.
Spanier, J. and Oldham, K. B. ``The Zeta Numbers and Related Functions.''
Ch. 3 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 25-33, 1987.
|
|
|
© 1996-9 Eric W. Weisstein