|
|
|
The Euler numbers, also called the Secant Numbers or Zig Numbers, are
defined for ![]() by
by
| (1) |
| (2) |
Some values of the Euler numbers are
The slightly different convention defined by
| (3) | |||
| (4) |
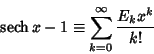 |
(5) |
| (6) |
To confuse matters further, the Euler Characteristic is sometimes also called the ``Euler number.''
See also Bernoulli Number, Eulerian Number, Euler Polynomial, Euler Zigzag Number, Genocchi Number
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Bernoulli and Euler Polynomials and the Euler-Maclaurin Formula.''
§23.1 in Handbook of Mathematical Functions with Formulas,
Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 804-806, 1972.
Conway, J. H. and Guy, R. K. In The Book of Numbers. New York: Springer-Verlag, pp. 110-111, 1996.
Guy, R. K. ``Euler Numbers.'' §B45 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 101, 1994.
Knuth, D. E. and Buckholtz, T. J. ``Computation of Tangent, Euler, and Bernoulli Numbers.'' Math. Comput. 21, 663-688, 1967.
Sloane, N. J. A. Sequences
A014547 and
A000364/M4019
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Spanier, J. and Oldham, K. B. ``The Euler Numbers,
![]() .'' Ch. 5 in An Atlas of Functions.
Washington, DC: Hemisphere, pp. 39-42, 1987.
.'' Ch. 5 in An Atlas of Functions.
Washington, DC: Hemisphere, pp. 39-42, 1987.
|
|
|
© 1996-9 Eric W. Weisstein