Let a closed surface have Genus  . Then the Polyhedral Formula becomes the
Poincaré Formula
. Then the Polyhedral Formula becomes the
Poincaré Formula
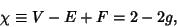 |
(1) |
where 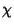 is the Euler characteristic, sometimes also known as the Euler-Poincaré
Characteristic. In terms of the Integral Curvature of the surface
is the Euler characteristic, sometimes also known as the Euler-Poincaré
Characteristic. In terms of the Integral Curvature of the surface 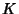 ,
,
 |
(2) |
The Euler characteristic is sometimes also called the Euler Number. It can also be expressed as
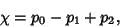 |
(3) |
where  is the
is the  th Betti Number of the space.
th Betti Number of the space.
See also Chromatic Number, Map Coloring
© 1996-9 Eric W. Weisstein
1999-05-25
![]() . Then the Polyhedral Formula becomes the
Poincaré Formula
. Then the Polyhedral Formula becomes the
Poincaré Formula